Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
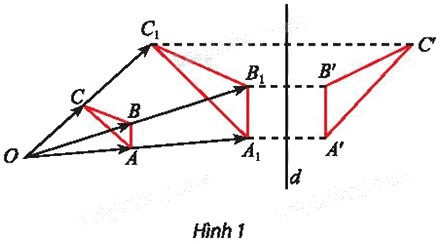
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: \(\left\{ \begin{array}{l}x' = kx + a\\y' = ky + b\end{array} \right.\) . Hãy chứng minh g là một phép đồng dạng.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Xét hai điểm bất kì \(M({x_1};{\rm{ }}{y_1}),{\rm{ }}N({x_2};{\rm{ }}{y_2})\) có ảnh qua g lần lượt là
Ta có \(\overrightarrow {MN} = \left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Và \(\overrightarrow {M'N'} = \left( {k{x_2} + a - k{x_1} - a;k{y_2} + b - k{y_1} - b} \right)\) \( = \left( {k\left( {{x_2} - {x_1}} \right);k\left( {{y_2} - {y_1}} \right)} \right)\)
Do đó \(\overrightarrow {M'N'} = k\left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Vì vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Suy ra \(M'N'{\rm{ }} = {\rm{ }}\left| k \right|.MN.\)
Vậy g là phép đồng dạng tỉ số \(\left| k \right|\).
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến ∆ABC thành \(\Delta \)\({A_1}{B_1}{C_1}\;\) và tìm phép biến hình biến \(\Delta \)\({A_1}{B_1}{C_1}\;\) thành \(\Delta \)A’B’C’.
⦁ Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A1B1C1, ta tìm phép biến hình biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Ta thấy các đường thẳng \(A{A_1},{\rm{ }}B{B_1},{\rm{ }}C{C_1}\;\) đồng quy tại O.
Xét phép vị tự tâm O, tỉ số k biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Suy ra \(\overrightarrow {O{A_1}} = k\overrightarrow {OA} \) và \(O{A_1}\; = {\rm{ }}\left| k \right|.OA.\)
Vì A, A1 nằm cùng phía đối với O nên k > 0.
Do đó \(k = \frac{{O{A_1}}}{{OA}}\).
Tương tự ta cũng có \(k = \frac{{O{B_1}}}{{OB}},k = \frac{{O{C_1}}}{{OC}}\)
Do đó \(k = \frac{{O{A_1}}}{{OA}} = \frac{{O{B_1}}}{{OB}} = \frac{{O{C_1}}}{{OC}}\)
Vì vậy \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) là phép biến hình biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}.\)
⦁ Để tìm phép biến hình biến \(\Delta {A_1}{B_1}{C_1}.\) thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến các điểm A1, B1, C1 theo thứ tự thành các điểm A’, B’, C’.
Ta thấy d là đường trung trực của đoạn A1A’.
Suy ra \({D_d}({A_1}){\rm{ }} = {\rm{ }}A'.\)
Chứng minh tương tự, ta được \({D_d}({B_1}){\rm{ }} = {\rm{ }}B';{\rm{ }}{D_d}({C_1}){\rm{ }} = {\rm{ }}C'.\)
Vì vậy Đd là phép biến hình biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vậy hai phép biến hình biến tam giác ABC thành tam giác A’B’C’ là \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) biến \(\Delta \)ABC thành \(\Delta \)A1B1C1 và \({D_d}\) biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
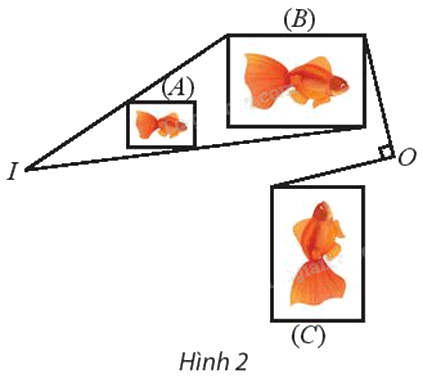
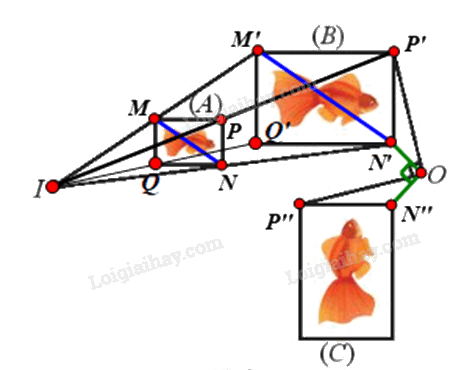
Tìm phép đồng dạng biến hình (A) thành hình (C).
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
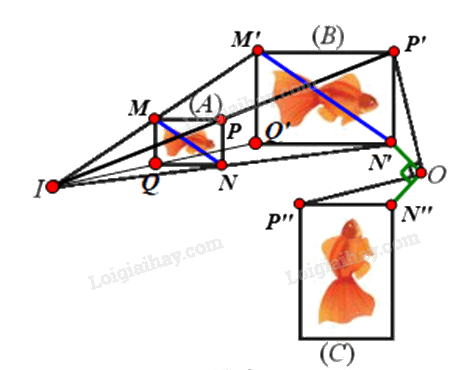
Gọi f là phép đồng dạng cần tìm.
⦁ Để tìm phép biến hình biến hình (A) thành hình (B), ta tìm phép biến hình biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta thấy các đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại I.
Xét phép vị tự tâm I, tỉ số k biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta có \({V_{(I,{\rm{ }}k)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra và
Vì M, M’ nằm cùng phía đối với I nên \(k{\rm{ }} > {\rm{ }}0.\)
Do đó \(k = \frac{{OM'}}{{OM}}.\)
Tương tự ta cũng có \(k = \frac{{ON'}}{{ON}},k = \frac{{OP'}}{{OP}},k = \frac{{OQ'}}{{OQ}}\)
Do đó \(k = \frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{OP'}}{{OP}} = \frac{{OQ'}}{{OQ}}\)
Vì vậy \({V_{\left( {I;\frac{{OM'}}{{OM}}} \right)}}\) là phép biến hình biến hình (A) thành hình (B).
⦁ Ta thấy OP’ = OP” và \(\widehat {P'OP''} = {90^o}\)
Suy ra phép quay tâm O, góc quay 90° biến điểm P’ thành điểm P”.
Chứng minh tương tự, ta thấy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) cũng biến các điểm khác trên hình (B) thành các điểm có vị trí tương ứng trên hình (C).
Vì vậy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) biến hình (B) thành hình (C).
⦁ Xét hai điểm N, P, ta có:
+) \(N' = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( N \right){\rm{, }}N''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'} \right);\)
+) \(P'{\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( P \right),P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {P'} \right).\)
Do đó:
+) \(N'P'{\rm{ }} = {\rm{ }}{V_{(I,{\rm{ }}k)}}\left( {NP} \right)\). Suy ra \(N'P'{\rm{ }} = {\rm{ }}k.NP;\)
+) \(N''P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'P'} \right).\)Suy ra \(N''P''{\rm{ }} = {\rm{ }}N'P'.\)
Vì vậy \(N''P'' = {\rm{ }}N'P'{\rm{ }} = {\rm{ }}k.NP.\)
Vậy f là phép đồng dạng tỉ số k \(\left( {k{\rm{ }} > {\rm{ }}0} \right)\) biến (A) thành (C) thỏa mãn \(\left( B \right){\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( {\left( A \right)} \right)\) và \(\left( C \right){\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {\left( B \right)} \right);\)
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến ∆ABC thành \(\Delta \)\({A_1}{B_1}{C_1}\;\) và tìm phép biến hình biến \(\Delta \)\({A_1}{B_1}{C_1}\;\) thành \(\Delta \)A’B’C’.
⦁ Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A1B1C1, ta tìm phép biến hình biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Ta thấy các đường thẳng \(A{A_1},{\rm{ }}B{B_1},{\rm{ }}C{C_1}\;\) đồng quy tại O.
Xét phép vị tự tâm O, tỉ số k biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Suy ra \(\overrightarrow {O{A_1}} = k\overrightarrow {OA} \) và \(O{A_1}\; = {\rm{ }}\left| k \right|.OA.\)
Vì A, A1 nằm cùng phía đối với O nên k > 0.
Do đó \(k = \frac{{O{A_1}}}{{OA}}\).
Tương tự ta cũng có \(k = \frac{{O{B_1}}}{{OB}},k = \frac{{O{C_1}}}{{OC}}\)
Do đó \(k = \frac{{O{A_1}}}{{OA}} = \frac{{O{B_1}}}{{OB}} = \frac{{O{C_1}}}{{OC}}\)
Vì vậy \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) là phép biến hình biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}.\)
⦁ Để tìm phép biến hình biến \(\Delta {A_1}{B_1}{C_1}.\) thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến các điểm A1, B1, C1 theo thứ tự thành các điểm A’, B’, C’.
Ta thấy d là đường trung trực của đoạn A1A’.
Suy ra \({D_d}({A_1}){\rm{ }} = {\rm{ }}A'.\)
Chứng minh tương tự, ta được \({D_d}({B_1}){\rm{ }} = {\rm{ }}B';{\rm{ }}{D_d}({C_1}){\rm{ }} = {\rm{ }}C'.\)
Vì vậy Đd là phép biến hình biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vậy hai phép biến hình biến tam giác ABC thành tam giác A’B’C’ là \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) biến \(\Delta \)ABC thành \(\Delta \)A1B1C1 và \({D_d}\) biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: \(\left\{ \begin{array}{l}x' = kx + a\\y' = ky + b\end{array} \right.\) . Hãy chứng minh g là một phép đồng dạng.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Xét hai điểm bất kì \(M({x_1};{\rm{ }}{y_1}),{\rm{ }}N({x_2};{\rm{ }}{y_2})\) có ảnh qua g lần lượt là
Ta có \(\overrightarrow {MN} = \left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Và \(\overrightarrow {M'N'} = \left( {k{x_2} + a - k{x_1} - a;k{y_2} + b - k{y_1} - b} \right)\) \( = \left( {k\left( {{x_2} - {x_1}} \right);k\left( {{y_2} - {y_1}} \right)} \right)\)
Do đó \(\overrightarrow {M'N'} = k\left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Vì vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Suy ra \(M'N'{\rm{ }} = {\rm{ }}\left| k \right|.MN.\)
Vậy g là phép đồng dạng tỉ số \(\left| k \right|\).
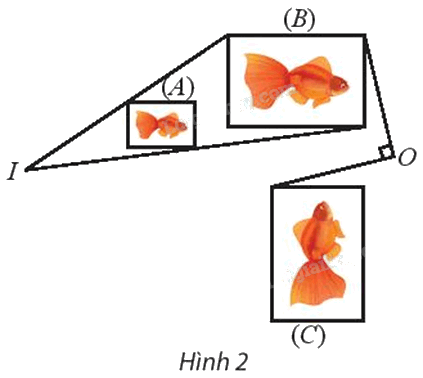
Tìm phép đồng dạng biến hình (A) thành hình (C).
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
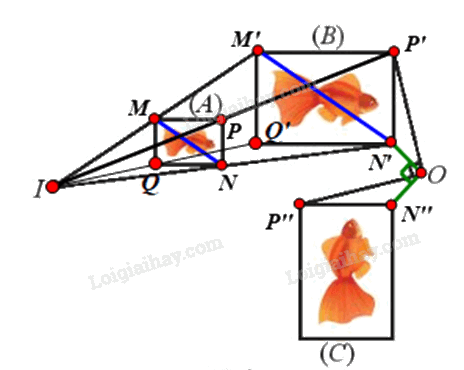
Gọi f là phép đồng dạng cần tìm.
⦁ Để tìm phép biến hình biến hình (A) thành hình (B), ta tìm phép biến hình biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta thấy các đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại I.
Xét phép vị tự tâm I, tỉ số k biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta có \({V_{(I,{\rm{ }}k)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra và
Vì M, M’ nằm cùng phía đối với I nên \(k{\rm{ }} > {\rm{ }}0.\)
Do đó \(k = \frac{{OM'}}{{OM}}.\)
Tương tự ta cũng có \(k = \frac{{ON'}}{{ON}},k = \frac{{OP'}}{{OP}},k = \frac{{OQ'}}{{OQ}}\)
Do đó \(k = \frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{OP'}}{{OP}} = \frac{{OQ'}}{{OQ}}\)
Vì vậy \({V_{\left( {I;\frac{{OM'}}{{OM}}} \right)}}\) là phép biến hình biến hình (A) thành hình (B).
⦁ Ta thấy OP’ = OP” và \(\widehat {P'OP''} = {90^o}\)
Suy ra phép quay tâm O, góc quay 90° biến điểm P’ thành điểm P”.
Chứng minh tương tự, ta thấy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) cũng biến các điểm khác trên hình (B) thành các điểm có vị trí tương ứng trên hình (C).
Vì vậy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) biến hình (B) thành hình (C).
⦁ Xét hai điểm N, P, ta có:
+) \(N' = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( N \right){\rm{, }}N''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'} \right);\)
+) \(P'{\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( P \right),P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {P'} \right).\)
Do đó:
+) \(N'P'{\rm{ }} = {\rm{ }}{V_{(I,{\rm{ }}k)}}\left( {NP} \right)\). Suy ra \(N'P'{\rm{ }} = {\rm{ }}k.NP;\)
+) \(N''P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'P'} \right).\)Suy ra \(N''P''{\rm{ }} = {\rm{ }}N'P'.\)
Vì vậy \(N''P'' = {\rm{ }}N'P'{\rm{ }} = {\rm{ }}k.NP.\)
Vậy f là phép đồng dạng tỉ số k \(\left( {k{\rm{ }} > {\rm{ }}0} \right)\) biến (A) thành (C) thỏa mãn \(\left( B \right){\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( {\left( A \right)} \right)\) và \(\left( C \right){\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {\left( B \right)} \right);\)
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Để hiểu rõ hơn về Mục 1 trang 38, 39, chúng ta cần xác định chính xác nội dung mà nó đề cập đến. Thông thường, đây có thể là các bài toán về:
Để giải các bài tập trong Mục 1 trang 38, 39 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Đề bài: Tìm tập xác định của hàm số y = √(2x - 1).
Lời giải:
Hàm số y = √(2x - 1) xác định khi và chỉ khi biểu thức dưới dấu căn không âm, tức là:
2x - 1 ≥ 0
⇔ 2x ≥ 1
⇔ x ≥ 1/2
Vậy, tập xác định của hàm số là D = [1/2; +∞).
Để học tập hiệu quả và đạt kết quả tốt trong môn Toán, học sinh cần lưu ý những điều sau:
Kiến thức về hàm số bậc hai và các phương pháp giải phương trình, bất phương trình bậc hai có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Việc giải các bài tập trong Mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán và đạt được kết quả tốt nhất.