Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác, dễ hiểu và nhiều tài liệu học tập hữu ích khác.
Mỗi đồ thị trong Hình 23 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy.
Đề bài
Mỗi đồ thị trong Hình 23 có chu trình Euler không? Nếu có hãy chỉ ra một chu trình như vậy.
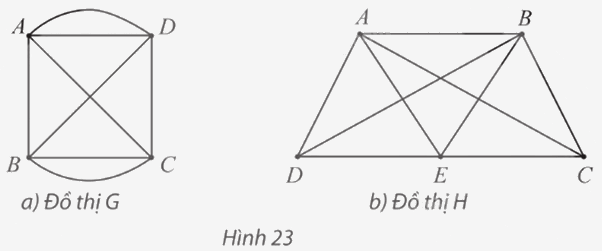
Phương pháp giải - Xem chi tiết
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết
⦁ Đồ thị G:
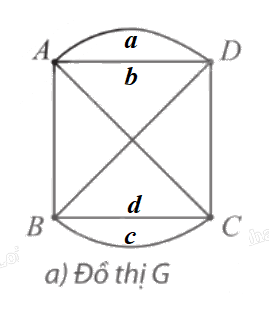
Ta có d(A) = d(B) = d(C) = d(D) = 4.
Suy ra đồ thị G có tất cả các đỉnh đều có bậc chẵn.
Vậy đồ thị G có chu trình Euler.
Chẳng hạn, ta có chu trình Euler: AabACDBcdBA.
⦁ Đồ thị H:
Ta có d(A) = d(B) = d(E) = 4; d(C) = d(D) = 3.
Suy ra đồ thị H có hai đỉnh C, D có bậc lẻ.
Vậy đồ thị H không có chu trình Euler.
Bài 1 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, cũng như khả năng vẽ đồ thị hàm số và phân tích các yếu tố ảnh hưởng đến đồ thị.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 58 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Xét hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, và khảo sát sự biến thiên của hàm số.
Giải:
| x | -∞ | 2 | +∞ |
|---|---|---|---|
| y' | - | 0 | + |
| y | -∞ | -1 | +∞ |
Học Toán 11 đòi hỏi sự kiên trì, chăm chỉ và phương pháp học tập đúng đắn. Hãy dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Đừng ngại đặt câu hỏi và thảo luận về các vấn đề chưa hiểu rõ. Chúc các em học tập tốt!