Chào mừng các em học sinh đến với bài học lý thuyết về các phép tính với số thập phân trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về số thập phân và cách thực hiện các phép tính cộng, trừ, nhân, chia với chúng.
Giaitoan.edu.vn tự hào là nền tảng học toán online uy tín, mang đến cho các em những bài giảng chất lượng, dễ hiểu và nhiều bài tập thực hành để củng cố kiến thức.
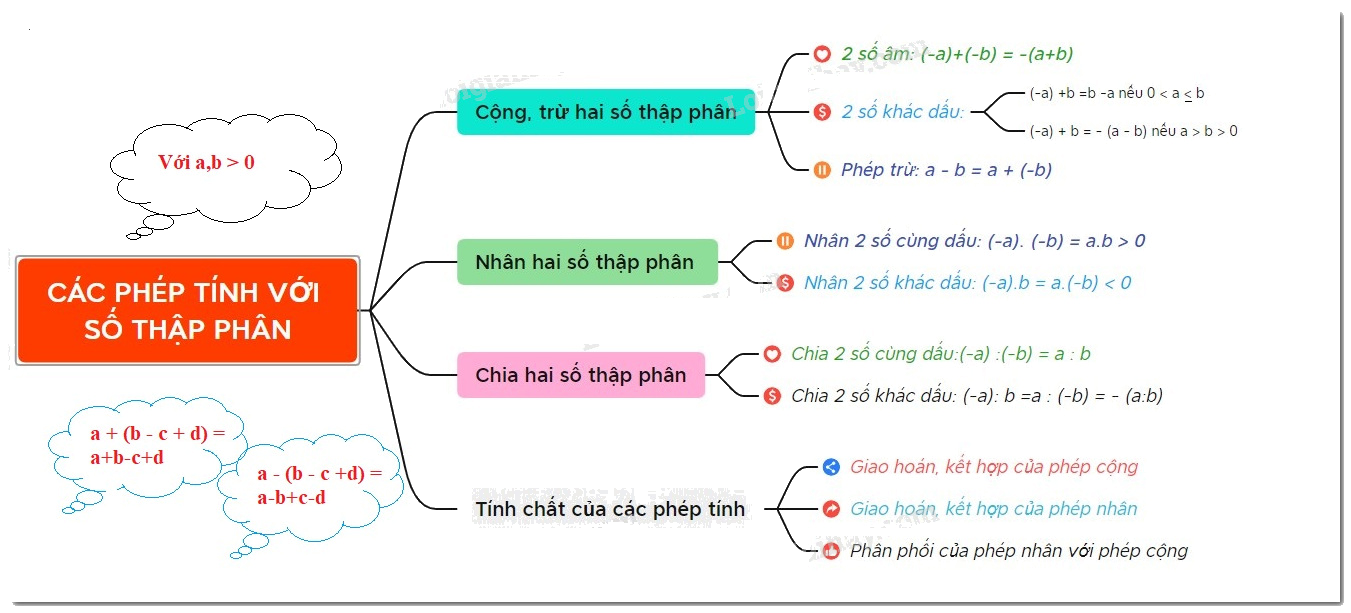
Lý thuyết Các phép tính với số thập phân Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Cộng hai số thập phân âm:
$ \left( { - a} \right) + \left( { - b} \right) = - \left( {a + b} \right)$ với $ a,\,\,b > 0$
Cộng hai số thập phân khác dấu:
$ \left( { - a} \right) + b = b - a$ nếu $ 0 < a \le b$ ;
$ \left( { - a} \right) + b = - \left( {a - b} \right)$ nếu $ a > b > 0$ .
Phép trừ hai số thập phân được đưa về phép cộng với số đối:
$ a - b = a + \left( { - b} \right)$ .
Ví dụ:
a) $ \left( { - 24,5} \right) + \left( { - 3,16} \right) = - \left( {24,5 + 3,16} \right) = - 27,66$
b) $ 1,5 - 3,169 = 1,5 + \left( { - 3,169} \right) = - \left( {3,169 - 1,5} \right) = - 1,669;$
c) $ 25,689 - \left( { - 1,2345} \right) = 25,689 + 1,2345 = 26,9235$ .
Nhân hai số cùng dấu:
$ \left( { - a} \right).\left( { - b} \right) = a.b$ với $ a,\,\,b > 0$ .
Nhân hai số khác dấu:
$ \left( { - a} \right).b = a.\left( { - b} \right) = - \left( {a.b} \right)$ với $ a,\,b > 0$ .
Ví dụ:
a) Nhân hai số nguyên cùng dấu:
$ \left( { - 1,25} \right).\left( { - 2,41} \right) = 1,25.2,41 = 3,0125$ .
b) Nhân hai số nguyên khác dấu:
$ 2,72.\left( { - 3,25} \right) = - \left( {2,72.3,25} \right) = - 8,84$ .
Chia hai số cùng dấu:
$ \left( { - a} \right):\left( { - b} \right) = a:b$ với $ a,\,\,b > 0$ .
Chia hai số khác dấu:
$ \left( { - a} \right):b = a:\left( { - b} \right) = - \left( {a:b} \right)$ với $ a,\,b > 0$ .
Ví dụ:
a) $ \left( {- 1,45} \right):\left( { - 2,5} \right) = 1,45:2,5 = 0,58$
b) $ \left( { - 5,24} \right):1,31 = - \left( {5,24:1,31} \right) = - 4$
Giống như các phép tính với số nguyên và phân số, các phép tính với số thập phân cũng có đầy đủ các tính chất như:
- Tính chất giao hoán và tính chất kết hợp của phép cộng.
- Tính chất giao hoán và tính chất kết hợp của phép nhân.
- Tính chất phân phối của phép nhân đối với phép cộng.
Vận dụng các tính chất của các phép tính với số thập phân và quy tắc dấu ngoặc, ta có thể tính giá trị các biểu thức một cách hợp lí.
Ví dụ:
$ \begin{array}{l}3,45 - 5,7 + 8,55 = \left( {3,45 + 8,55} \right) - 5,7\\ = 12 - 5,7 = 6,3\end{array}$
Số thập phân là một phần quan trọng trong chương trình Toán 6, là nền tảng cho các kiến thức toán học nâng cao hơn. Hiểu rõ lý thuyết và nắm vững các quy tắc thực hiện các phép tính với số thập phân là điều cần thiết để các em học sinh có thể giải quyết các bài toán một cách chính xác và hiệu quả.
Số thập phân là cách biểu diễn các số không nguyên bằng cách sử dụng dấu phẩy (,) để phân tách phần nguyên và phần thập phân. Ví dụ: 3,5; 0,75; 12,01 là các số thập phân.
Các phép tính cộng, trừ, nhân, chia với số thập phân được thực hiện theo các quy tắc sau:
Để cộng hoặc trừ các số thập phân, ta thực hiện các bước sau:
Ví dụ:
| Phép tính | Kết quả |
|---|---|
| 3,5 + 2,7 | 6,2 |
| 5,8 - 1,3 | 4,5 |
Để nhân các số thập phân, ta thực hiện các bước sau:
Ví dụ:
2,5 x 1,2 = 3,0
Để chia các số thập phân, ta thực hiện các bước sau:
Ví dụ:
10,5 : 0,5 = 21 (vì 10,5 x 10 = 105 và 0,5 x 10 = 5)
Hy vọng bài học lý thuyết này sẽ giúp các em hiểu rõ hơn về các phép tính với số thập phân trong chương trình Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt!