Chào mừng bạn đến với bài tổng hợp lý thuyết quan trọng về các hình tứ giác đặc biệt trong chương trình Toán 6 Chân trời sáng tạo. Bài viết này sẽ cung cấp kiến thức nền tảng, các định nghĩa, tính chất và dấu hiệu nhận biết của từng hình, giúp bạn học tập hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và dễ hiểu.
Lý thuyết Hình chữ nhật- Hình thoi- Hình bình hành- Hình thang cân Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
1. Nhận biết hình chữ nhật
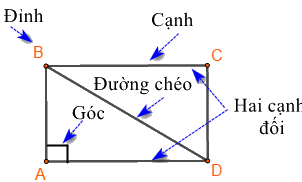
Hình chữ nhật \(ABCD\) có:
- Bốn đỉnh A, B, C, D
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,\,BC = AD\).
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
\(AC = BD\) và \(OA = OC;\,\,OB = OD\).
2.Cách vẽ hình chữ nhật
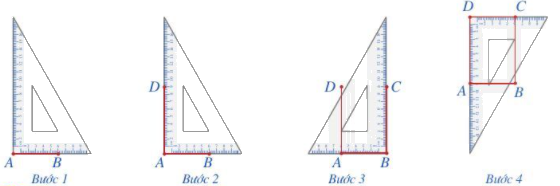
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm
Bước 4. Vẽ đoạn thẳng CD.
1. Nhận biết hình thoi
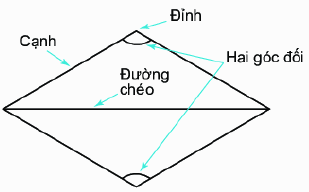
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\)
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
2. Vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi \(ABCD\), biết \(AB = 5\,cm\) và \(AC = 8\,cm\).
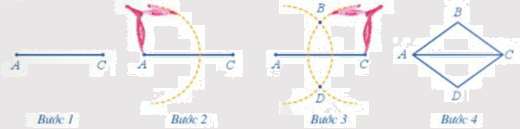
Bước 1. Dùng thước vẽ đoạn thẳng \(AC = 8\,cm\)
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính \(5\,cm\).
Bước 3.Dùng compa vẽ một phần đường tròn tâm C bán kính \(5\,cm\); phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.
1.Nhận biết hình bình hành
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).
- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: \(OA = OC;\,OB = OD.\)
- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
2.Cách vẽ hình bình hành
Cách vẽ hình bình hành có hai cạnh là a và b:
Bước 1: Vẽ đoạn thẳng \(AB = a\left( {cm} \right)\)
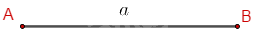
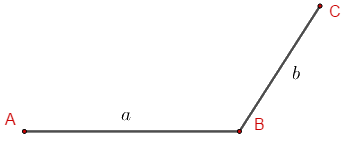
Bước 2: Vẽ đường thẳng đi qua \(B\). Lấy điểm \(C\) trên đường thẳng đó sao
cho \(BC = b\left( {cm} \right)\)
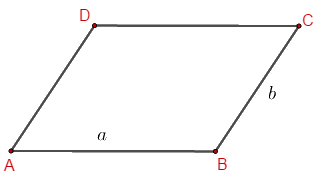
Bước 3: Vẽ đường thẳng đi qua \(A\) và song song với cạnh \(BC\), đường thẳng qua \(C\) và song song với \(AB\). Hai đường thẳng này cắt nhau tại \(D\), ta được hình bình hành \(ABCD\).
1. Nhận biết hình thang cân
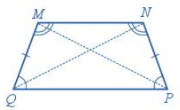
Hình thang cân \(MNPQ\) có:
Hai cạnh cạnh bên song song: \(MN\) song song với \(PQ\).
- Hai cạnh bên bằng nhau: \(MQ = NP\).
- Hai đường chéo bằng nhau: \(MP = NQ\).
- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau, tức là hai góc \(NPQ\) và \(PQM\) bằng nhau; hai góc kề với cạnh bên \(MN\) bằng nhau, tức là hai góc \(QMN\) và \(MNP\) bằng nhau.
2.Cách gấp hình thang cân
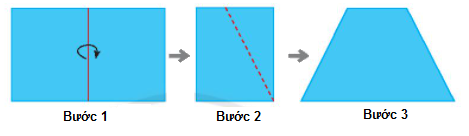
Bước 1: Gấp đôi một tờ giấy hình chữ nhật
Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (Cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3: Mở tờ giấy ra ta được một hình thang cân.
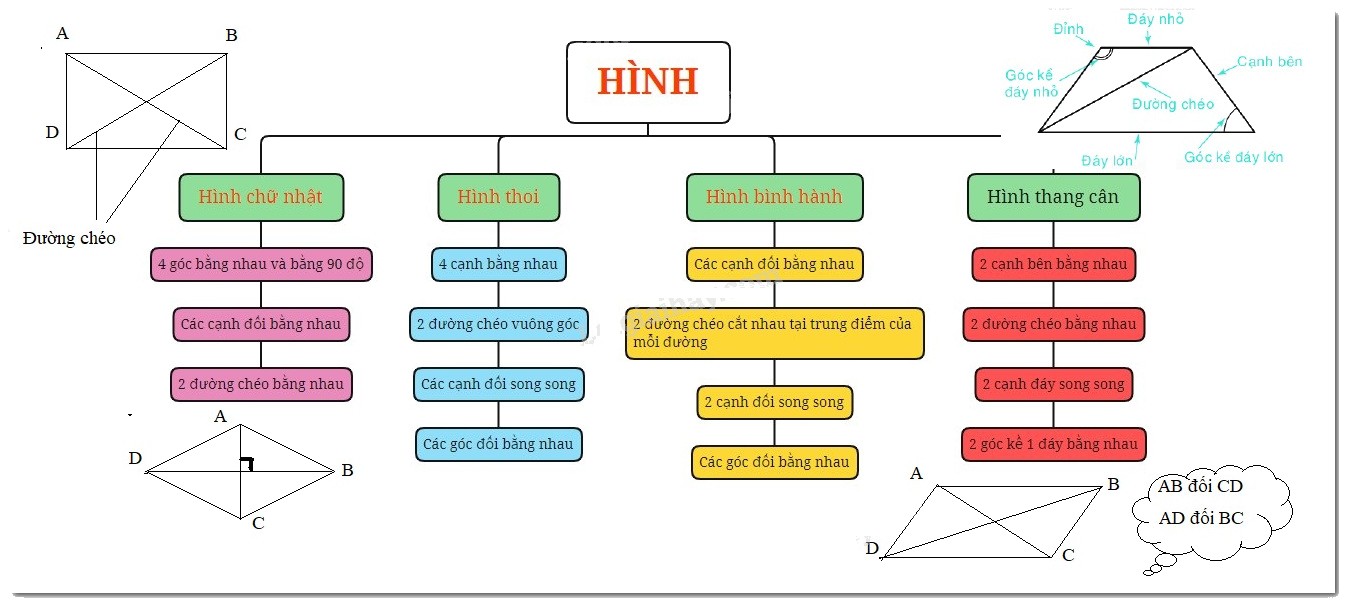
Trong chương trình Toán 6, việc nắm vững kiến thức về các hình tứ giác đặc biệt như hình chữ nhật, hình thoi, hình bình hành và hình thang cân là vô cùng quan trọng. Dưới đây là tổng hợp lý thuyết chi tiết, giúp các em học sinh hiểu rõ hơn về các khái niệm này.
Định nghĩa: Hình chữ nhật là hình tứ giác có bốn góc vuông.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình thoi là hình tứ giác có bốn cạnh bằng nhau.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình bình hành là hình tứ giác có các cạnh đối song song.
Tính chất:
Dấu hiệu nhận biết:
Định nghĩa: Hình thang cân là hình thang có hai cạnh bên bằng nhau.
Tính chất:
Dấu hiệu nhận biết:
Xét hình chữ nhật ABCD, ta có AB = CD và AD = BC. Các góc A, B, C, D đều bằng 90 độ. Đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
Hy vọng với bài tổng hợp lý thuyết này, các em học sinh sẽ có thêm kiến thức và tự tin hơn trong việc giải các bài tập về hình học. Chúc các em học tốt!