Chào mừng các em học sinh đến với bài học về Lý thuyết Điểm. Đường thẳng trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về điểm, đường thẳng, đoạn thẳng và tia.
Giaitoan.edu.vn tự hào là nền tảng học toán online uy tín, cung cấp nội dung chất lượng cao và phương pháp học tập hiệu quả, giúp các em học tập tốt môn Toán.
Lý thuyết Điểm. Đường thẳng Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Bài 1. Điểm. Đường thẳng
1. Điểm
Mỗi chấm nhỏ trên trang giấy cho ta hình ảnh của một điểm.
Người ta thường dùng các chữ các in hoa A, B, C, ... để đặt tên cho điểm.
Chú ý:
• Khi nói tới hai điểm mà không giải thích gì thêm, ta coi đó là hai điểm phân biệt.
• Từ những điểm ta xây dựng được các hình. Mỗi hình là một tập hợp các điểm. Một điểm cũng được coi là một hình.
2. Đường thẳng
Dùng bút kẻ một vạch thẳng dọc theo mép thước ta sẽ đường hình ảnh của một đường thẳng.
Tương tự, dây điện kéo căng, mép tường, ... cho ta hình ảnh của đường thẳng. Đường thẳng không bị giới hạn về hai phía.
Chú ý: Người ta dùng các chữ cái in thường a, b, c, d, ... để đặt tên cho các đường thẳng.
3. Vẽ đường thẳng
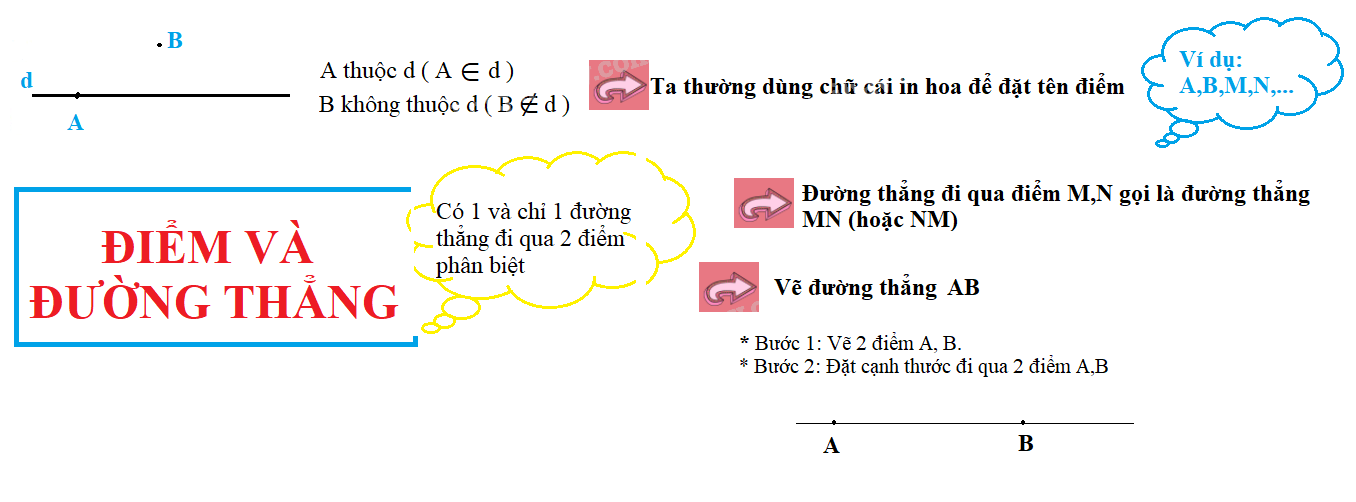
Vẽ hai điểm A và B trên giấy. Đặt cạnh thước đi qua hai điểm A và B.
Dùng đầu bút vạch thẳng theo cạnh thước, ta được hình ảnh đường thẳng đi qua hai điểm A và B
Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt cho trước.
4. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng
• Vẽ một điểm A trên giấy, dùng thước thẳng vẽ đường thẳng d đi qua điểm A. Khi đó, ta nói điểm A thuộc đường thẳng d ( hoặc đường thẳng d chứa điểm A, hoặc điểm A nằm trên đường thẳng d), kí hiệu là: A \( \in \) d.
• Dùng thước thẳng vẽ đường thẳng d không đi qua điểm B.
Khi đó, ta nói điểm B không thuộc đường thẳng d ( hoặc đường thẳng d không chứa điểm B, hoặc điểm B không nằm trên đường thẳng d), kí hiệu là: B \( \notin \) d.
Chú ý: Nếu trên đường thẳng a có hai điểm A và B, ta cũng có thể gọi tên đường thẳng đó là đường thẳng AB hay BA.
Trong chương trình Toán 6, việc nắm vững kiến thức về điểm, đường thẳng, đoạn thẳng và tia là nền tảng quan trọng cho các bài học tiếp theo. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và bài tập thực hành để giúp các em học sinh hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Điểm là một khái niệm cơ bản trong hình học. Điểm không có kích thước, chỉ xác định vị trí. Chúng ta thường ký hiệu điểm bằng một chữ cái in hoa, ví dụ: A, B, C,...
Đường thẳng là một đường đi thẳng không bị giới hạn về hai phía. Một đường thẳng được xác định bởi hai điểm phân biệt. Chúng ta thường ký hiệu đường thẳng bằng một chữ cái in thường, ví dụ: a, b, c,...
Đoạn thẳng là một phần của đường thẳng được giới hạn bởi hai điểm. Hai điểm giới hạn đoạn thẳng được gọi là hai mút của đoạn thẳng. Độ dài của đoạn thẳng là khoảng cách giữa hai mút của nó.
Tia là một phần của đường thẳng được giới hạn bởi một điểm. Điểm giới hạn tia được gọi là gốc của tia. Tia có một mút và kéo dài vô tận về một phía.
Để so sánh độ dài hai đoạn thẳng, ta có thể sử dụng thước đo hoặc áp dụng tính chất bắc cầu. Tính chất bắc cầu phát biểu như sau: Nếu AB < BC và BC < CD thì AB < CD.
Trung điểm của đoạn thẳng là điểm nằm giữa hai mút của đoạn thẳng và cách đều hai mút đó. Nếu M là trung điểm của đoạn thẳng AB thì AM = MB = AB/2.
Ngoài những kiến thức cơ bản trên, các em có thể tìm hiểu thêm về các khái niệm liên quan như đường tròn, góc, và các tính chất của hình học phẳng. Việc nắm vững những kiến thức này sẽ giúp các em giải quyết các bài toán phức tạp hơn trong chương trình Toán 6 và các lớp học tiếp theo.
Để củng cố kiến thức, các em nên luyện tập thêm các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham gia các khóa học online hoặc tìm kiếm sự giúp đỡ từ các thầy cô giáo.
Lý thuyết Điểm. Đường thẳng là một phần quan trọng trong chương trình Toán 6. Việc hiểu rõ và áp dụng kiến thức này sẽ giúp các em học tập tốt môn Toán và xây dựng nền tảng vững chắc cho các bài học tiếp theo. Chúc các em học tập tốt!