Bài học này cung cấp kiến thức nền tảng về làm tròn số thập phân và ước lượng kết quả, một trong những chủ đề quan trọng của chương trình Toán 6 Chân trời sáng tạo. Học sinh sẽ được hướng dẫn chi tiết cách làm tròn số thập phân đến hàng nào đó và ứng dụng vào việc ước lượng kết quả của các phép tính.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng.
Lý thuyết Làm tròn số thập phân và ước lượng kết quả Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
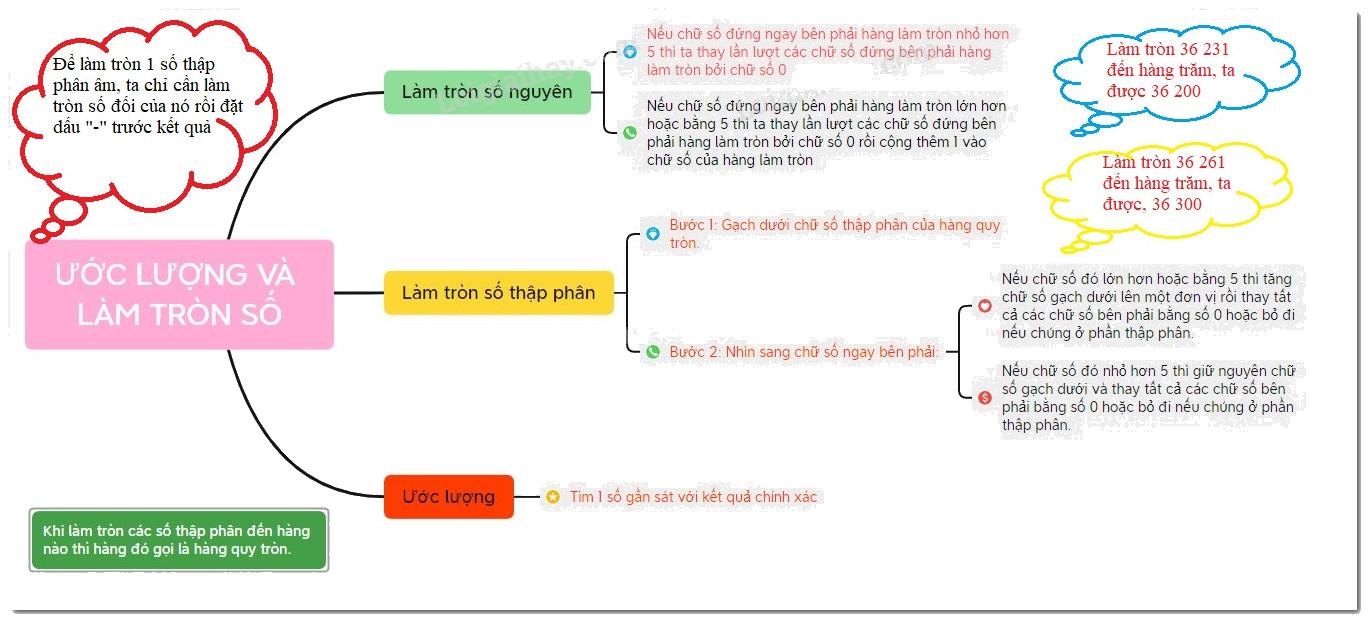
Để làm tròn một số nguyên (có nhiều chữ số) đến một hàng nào đó, ta làm như sau:
- Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn $5$ thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số $0$.
- Nếu chữ số đứng ngay bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số $0$ rồi cộng thêm $1$ vào chữ số của hàng làm tròn.
Chú ý: Kí hiệu “ ” đọc là “gần bằng” hoặc “xấp xỉ”.
Ví dụ:
Làm tròn số $125\,\,356$ đến hàng nghìn
Do chữ số hàng trăm là $3$ nên: $125\,\,356 \approx 125\,\,000$
Để làm tròn một số thập phân dương đến một hàng nào đấy (gọi là hàng làm tròn), ta làm như sau:
- Đối với chữ số hàng làm tròn:
- Đối với các chữ số sau hàng làm tròn:
Ví dụ:
Làm tròn số $24,037$ đến hàng phần mười (đến chữ số thập phân thứ nhất).
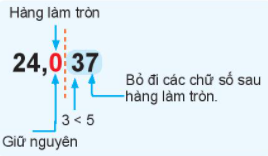
Làm tròn số đến hàng phần mười ta được kết quả là $24,0$
Vậy: $24,037 \approx 24,0$.
Ta có thể sử dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí.
Ví dụ:
Ước lượng kết quả các phép tính sau:
a) $\left( { - 11,032} \right).\left( { - 24,3} \right) \approx 11.24 = 264$
b) $81.49 \approx 80.50 = 4\,000$
Trong chương trình Toán 6 Chân trời sáng tạo, việc làm quen với các khái niệm về số thập phân và các phép toán liên quan là vô cùng quan trọng. Một trong những kỹ năng cần thiết là làm tròn số thập phân và ước lượng kết quả. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết này.
Làm tròn số thập phân là việc thay thế một số thập phân bằng một số thập phân gần nhất với nó, nhưng có ít chữ số thập phân hơn. Mục đích của việc làm tròn là để đơn giản hóa số, giúp việc tính toán và ước lượng trở nên dễ dàng hơn.
Để làm tròn một số thập phân đến một hàng nào đó, ta thực hiện theo các bước sau:
Ví dụ:
Ước lượng kết quả là việc tìm một giá trị gần đúng cho kết quả của một phép tính. Việc ước lượng giúp ta kiểm tra tính hợp lý của kết quả và có thể sử dụng trong các tình huống thực tế khi không cần độ chính xác tuyệt đối.
Để ước lượng kết quả của một phép tính, ta thường làm tròn các số trong phép tính đến một hàng nào đó (ví dụ: hàng đơn vị, hàng chục) trước khi thực hiện phép tính.
Ví dụ:
Ước lượng kết quả của phép tính 3,14 x 5,8:
Kết quả chính xác của phép tính là 18,202. Như vậy, ước lượng của chúng ta khá gần với kết quả thực tế.
Kỹ năng làm tròn số thập phân và ước lượng kết quả có nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức, hãy thực hiện các bài tập sau:
Làm tròn số thập phân và ước lượng kết quả là những kỹ năng quan trọng trong Toán học và có nhiều ứng dụng trong cuộc sống. Việc nắm vững lý thuyết và thực hành thường xuyên sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán và các tình huống thực tế.