Giải bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2

Bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng thực hành phép tính với số nguyên. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Đường nét đứt có phải là trục đối xứng của mỗi hình sau không?..

Đề bài

Đường nét đứt có phải là trục đối xứng của mỗi hình sau không?

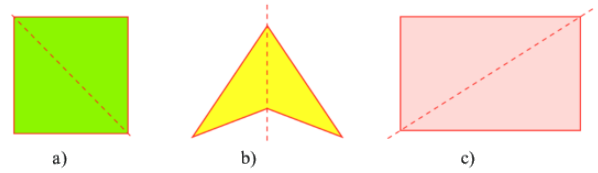
Giải bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 1

Phương pháp giải - Xem chi tiết Giải bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 2

Hình có trục đối xứng là hình tồn tại một đường thẳng chia hình thành 2 phần sao cho hai phần của hình chồng khít lên nhau. Đường thẳng trên là trục đối xứng của hình đó.

Lời giải chi tiết

Ở hình a,b: Các đường nét đứt là trục đối xứng của các hình trên vì nếu gấp hình theo đường nét đứt, ta được 2 phần hình chồng khít lên nhau.

Ở hình c: Đường nét đứt không là trục đối xứng của hình vì nếu gấp hình theo đường nét đứt, ta không được 2 phần hình chồng khít lên nhau.

Tự tin bứt phá năm học lớp 6 ngay từ đầu! Khám phá Giải bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 – nội dung then chốt trong chuyên mục giải sgk toán 6 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, cập nhật chính xác theo khung chương trình sách giáo khoa THCS, đây chính là người bạn đồng hành đáng tin cậy giúp các em tối ưu hóa toàn diện quá trình ôn luyện và xây dựng nền tảng kiến thức Toán vững chắc thông qua phương pháp tiếp cận trực quan, mang lại hiệu quả vượt trội không ngờ.

Giải bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2: Tổng quan

Bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 thuộc chương học về số nguyên. Bài tập này tập trung vào việc thực hành các phép cộng, trừ số nguyên, đặc biệt là các bài toán có liên quan đến số âm. Việc nắm vững kiến thức về số nguyên là nền tảng quan trọng cho các chương học tiếp theo của môn Toán 6.

Nội dung bài tập

Bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:

Tính giá trị của các biểu thức chứa phép cộng, trừ số nguyên.
Giải các bài toán có tình huống thực tế liên quan đến số nguyên (ví dụ: tính nhiệt độ, độ cao, số tiền nợ,...).
So sánh các số nguyên.

Phương pháp giải bài tập

Để giải bài tập về số nguyên một cách hiệu quả, học sinh cần nắm vững các quy tắc sau:

Quy tắc cộng hai số nguyên cùng dấu: Cộng hai số nguyên cùng dấu, ta cộng các giá trị tuyệt đối của chúng và giữ nguyên dấu.
Quy tắc cộng hai số nguyên khác dấu: Cộng hai số nguyên khác dấu, ta lấy giá trị tuyệt đối của số lớn trừ giá trị tuyệt đối của số nhỏ và giữ nguyên dấu của số lớn.
Quy tắc trừ hai số nguyên: Trừ một số nguyên là cộng với số đối của nó.
Quy tắc so sánh hai số nguyên: Số nguyên âm nhỏ hơn số nguyên dương. Trong hai số nguyên âm, số nào có giá trị tuyệt đối lớn hơn thì nhỏ hơn.

Lời giải chi tiết bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2

Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 2 trang 55. Tuy nhiên, dựa trên cấu trúc chung của sách, chúng ta có thể đưa ra một ví dụ minh họa:

Ví dụ:

Tính: a) (-5) + 8; b) 12 + (-3); c) (-7) - 4; d) 9 - (-2)

Giải:

a) (-5) + 8 = 3 (Cộng hai số nguyên khác dấu, lấy 8 - 5 = 3 và giữ dấu của số lớn là dương)
b) 12 + (-3) = 9 (Cộng hai số nguyên khác dấu, lấy 12 - 3 = 9 và giữ dấu của số lớn là dương)
c) (-7) - 4 = (-7) + (-4) = -11 (Trừ một số nguyên là cộng với số đối của nó)
d) 9 - (-2) = 9 + 2 = 11 (Trừ một số nguyên là cộng với số đối của nó)

Mở rộng và bài tập tương tự

Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự sau:

Tính: a) (-10) + 5; b) 15 + (-7); c) (-8) - 2; d) 6 - (-4)
Một người nông dân có 5000 đồng. Anh ta mua 2000 đồng tiền phân bón và sau đó lại nợ thêm 1000 đồng của hàng xóm. Hỏi người nông dân còn lại bao nhiêu tiền?

Lưu ý khi giải bài tập

Khi giải bài tập về số nguyên, học sinh cần:

Đọc kỹ đề bài để hiểu rõ yêu cầu.
Xác định đúng dấu của các số nguyên.
Áp dụng đúng các quy tắc cộng, trừ số nguyên.
Kiểm tra lại kết quả sau khi giải xong.

Kết luận

Bài 2 trang 55 SGK Toán 6 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về số nguyên. Bằng cách luyện tập thường xuyên và áp dụng đúng các quy tắc, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.