Chào mừng các em học sinh đến với bài học về Lý thuyết Chu vi và Diện tích trong chương trình Toán 6 Chân trời sáng tạo. Đây là một trong những kiến thức nền tảng quan trọng, giúp các em hiểu rõ hơn về các khái niệm hình học cơ bản và ứng dụng vào giải quyết các bài toán thực tế.
Bài học này sẽ cung cấp cho các em những kiến thức cơ bản về chu vi và diện tích của các hình như hình vuông, hình chữ nhật, hình tròn, cùng với các công thức tính toán và ví dụ minh họa.
Lý thuyết Chu vi và diện tích của một số hình trong thực tiễn Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
I. Thế nào là chu vi và diện tích
1. Chu vi
Chu vi của một hình bất kì là độ dài phần đường thẳng bao quanh hình đó.
2. Diện tích
Diện tích của một hình là toàn bộ phần bên trong của hình đó.
Cho hình vuông có cạnh bằng \(a\):
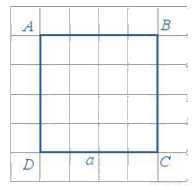
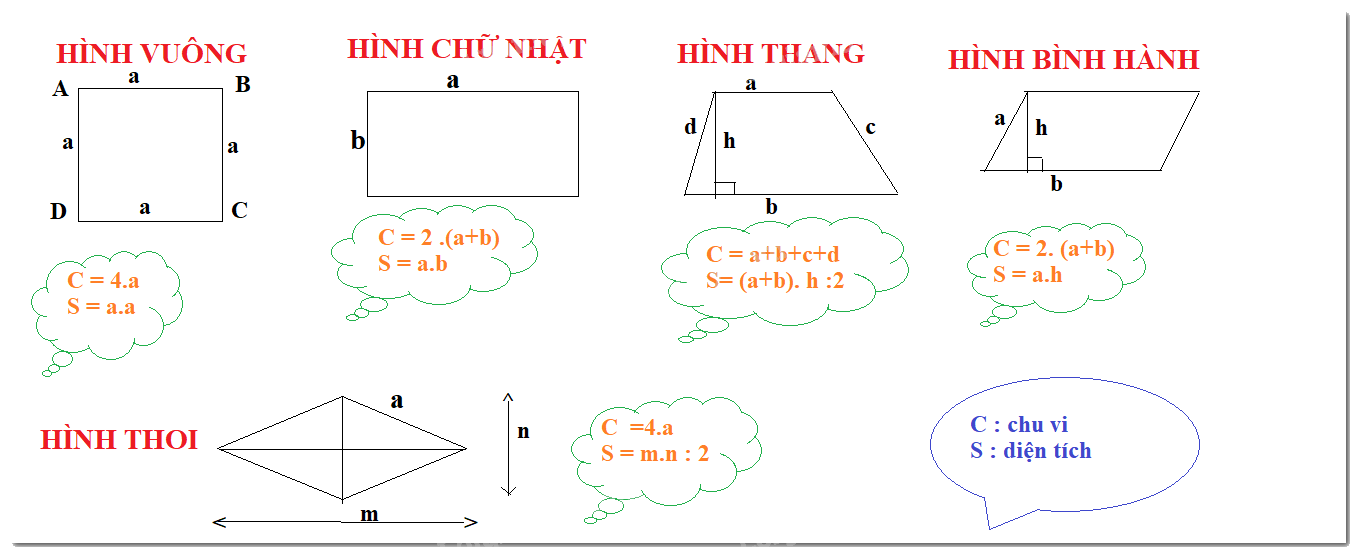
Chu vi hình vuông là: \(C = 4a\)
Diện tích hình vuông là: \(S = a.a = {a^2}\).
Ví dụ:
Một mảnh ruộng hình vuông có cạnh bằng \(15\,m\). Năng suất lúa là \(0,9\,kg/{m^2}\). Tính diện tích mảnh ruộng và sản lượng thu hoạch được.
Diện tích mảnh ruộng hình vuông là: \({15^2} = 225\,({m^2})\).
Sản lượng thu hoạch được là: \(225:0,9 = 312,5\)(kg).
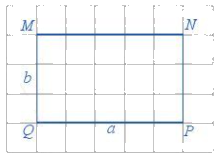
Chu vi của hình chữ nhật là: \(C = 2\left( {a + b} \right);\)
Diện tích của hình chữ nhật là: \(S = a.b\)
Chú ý: Khi tính chu vi và diện tích thì chiều dài và chiều rộng phải cùng đơn vị đo.
Ví dụ 1:
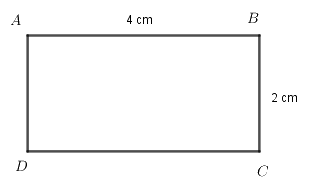
Chu vi hình chữ nhật \(ABCD\) là: \(2.(4 + 2) = 12\,\,(c{m})\).
Diện tích hình chữ nhật \(ABCD\) là: \(4.2 = 8\,(c{m^2})\).
Ví dụ 2:
Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?
Giải:
Diện tích căn phòng hình chữ nhật là: \(8.6 = 48\,({m^2})\)
Diện tích của một viên gạch là: \(20.50 = 1000\,(c{m^2}) = 0,1\,({m^2})\)
Số viên gạch bác Khôi cần dùng là: \(48:0,1 = 480\) (viên).
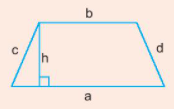
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
\(P = a + b + c + d\)
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
\(S = \frac{{(a + b).h}}{2}\)
Chú ý: Cách làm trên vẫn áp dụng được để tính chu vi và diện tích hình thang cân.
Ví dụ:
Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.
Diện tích hình thang cân là: \(\frac{{(5 + 3,5).4}}{2} = 17\) (\(c{m^2}\)).
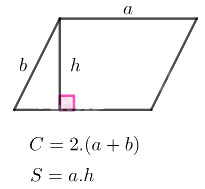
Chu vi hình bình hành : \(C = 2(a + b)\).
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
Chú ý: Khi tính chu vi và diện tích hình bình hành phải đưa các độ dài về cùng đơn vị đo.
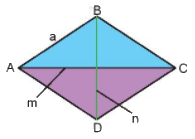
Chu vi hình thoi bằng độ dài cạnh nhân với bốn: \(C = 4a\)
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
Ví dụ:
Hình thoi có độ dài hai đường chéo là 40 m và 20 m có diện tích là:
\(S = \frac{{40.20}}{2} = 400\,\,({m^2})\).
a) Tính chu vi của một số hình trong thực tiễn:
Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó
b) Tính diện tích của một số hình trong thực tiễn:
- Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi,…thì ta áp dụng công thức và tính.
- Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi,…
Ví dụ:
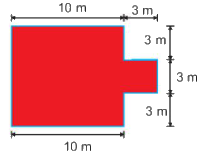
Người ta cần xây tường rào và lát cỏ cho một khu vui chơi như hình bên. Mỗi mét tường tốn 150 nghìn đồng, mỗi mét vuông cỏ tốn 100 nghìn đồng. Hỏi người ta cần tất cả bao nhiêu tiền để xây tường rào và lát cỏ cho một khu vui chơi?
Giải
Khu vui chơi gồm bốn mặt, hai mặt 10 m, một mặt 9m và 1 mặt gồm năm cạnh 3 m nên:
Chu vi khu vui chơi là: \(10.2 + 3.5 + 9 = 44\) (m)
=> Số tiền để xây tường rào là: \(150\,000\,.\,44 = \,6\,\,600\,000\) (đồng).
Diện tích khu vui chơi bằng tổng của một hình chữ nhật có chiều dài 10 m và chiều rộng 9m và một hình vuông có cạnh bằng 3 m:
\(S = 10.9 + {3^2} = 99\)(\({m^2}\))
=> Số tiền để lát cỏ là: \(100\,000.99 = 9\,\,900\,000\) (đồng).
Chu vi và diện tích là hai khái niệm cơ bản trong hình học, được sử dụng để đo lường kích thước của các hình phẳng. Hiểu rõ về chu vi và diện tích là nền tảng quan trọng để giải quyết các bài toán liên quan đến hình học trong chương trình Toán 6 Chân trời sáng tạo và các lớp học cao hơn.
Chu vi của một hình là tổng độ dài của tất cả các cạnh của hình đó. Đơn vị đo chu vi thường là mét (m), centimet (cm), milimet (mm),...
Diện tích của một hình là số đo bề mặt của hình đó. Đơn vị đo diện tích thường là mét vuông (m²), centimet vuông (cm²), milimet vuông (mm²),...
Hình vuông là hình có bốn cạnh bằng nhau và bốn góc vuông. Gọi độ dài một cạnh của hình vuông là a.
Hình chữ nhật là hình có bốn góc vuông và hai cặp cạnh đối diện bằng nhau. Gọi chiều dài của hình chữ nhật là l và chiều rộng là w.
Hình tròn là tập hợp tất cả các điểm cách một điểm cố định (tâm) một khoảng không đổi (bán kính). Gọi bán kính của hình tròn là r.
Chu vi và diện tích được ứng dụng rộng rãi trong đời sống hàng ngày:
Dưới đây là một số bài tập vận dụng để giúp các em hiểu rõ hơn về lý thuyết chu vi và diện tích:
Khi tính chu vi và diện tích, các em cần chú ý đến đơn vị đo. Nếu các cạnh của hình có đơn vị đo khác nhau, các em cần đổi về cùng một đơn vị trước khi tính toán.
Hy vọng bài học này đã giúp các em nắm vững kiến thức về lý thuyết chu vi và diện tích. Chúc các em học tập tốt!