Chào mừng các em học sinh đến với bài học về Lý thuyết Xác suất thực nghiệm trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ giúp các em hiểu rõ khái niệm xác suất, cách tính xác suất thực nghiệm và ứng dụng của nó trong thực tế.
Giaitoan.edu.vn cung cấp kiến thức toán học lớp 6 một cách dễ hiểu, trực quan, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Lý thuyết Xác suất thực nghiệm Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
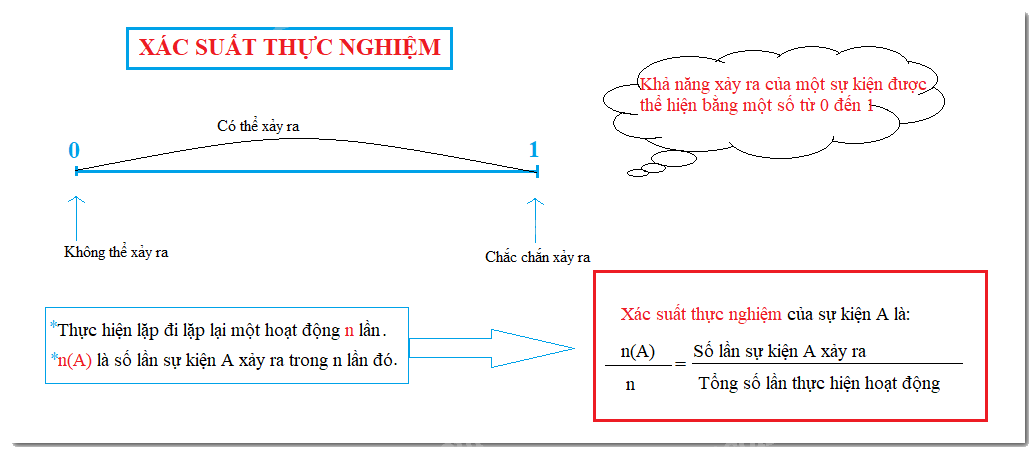
Ta đã biết khi thực hiện một phép thử nghiệm, một sự kiện có thể hoặc không thể xảy ra. Để nói về khả năng xảy ra của một sự kiện, ta dùng một con số có giá trị từ 0 đến 1.
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
\(\frac{{n(A)}}{n} = \) Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
Được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.
Tung hai đồng xu cân đối 50 lần ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện:
a) Có một đồng xu sấp, một đồng xu ngửa.
b) Hai đồng xu đều ngửa.
Giải:
a) Số lần nhận được một đồng xu sấp, một đồng xu ngửa là 24 lần.
Tổng số lần thực hiện thí nghiệm là 50.
Xác suất thực nghiệm của sự kiện “có một đồng xu sấp, một đồng xu ngửa” là:
\(\dfrac{{24}}{{50}} = 0,48\).
b) Số lần nhận được hai đồng xu đều ngửa là 14.
Tổng số lần thực hiện thí nghiệm là 50.
Xác suất thực nghiệm của sự kiện “hai đồng xu đều ngửa” là:
\(\dfrac{{14}}{{50}} = 0,28\).
Phương pháp:
Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.
Bước 2: Sử dụng công thức sau để tính xác suất
Ví dụ:
Gieo một con xúc xắc sáu mặt 7 lần và số chấm xuất hiện của mỗi lần gieo như sau:
Lần 1 | Lần 2 | Lần 3 | Lần 4 | Lần 5 | Lần 6 | Lần 7 |
1 | 1 | 5 | 6 | 3 | 3 | 4 |
Bước 1: Số lần gieo được mặt 3 chấm là 2 lần. Tổng số lần gieo là 7.
Bước 2: Xác suất mặt 3 chấm xuất hiện là \(\dfrac{2}{7}\)
Bài 1. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
Số lần | 8 | 7 | 3 | 12 | 10 | 10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
A. 0,21
B. 0,44
C. 0,42
D. 0,18
Lời giải: Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8+3+10=21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
\(\dfrac{{21}}{{50}} = 0,42\)
Chọn đáp án C
Bài 2. Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
A. \(\dfrac{7}{{11}}\)
B. \(\dfrac{4}{{11}}\)
C. \(\dfrac{4}{7}\)
D. \(\dfrac{3}{7}\)
Lời giải:
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là: \(\dfrac{{14}}{{22}} = \dfrac{7}{{11}}\)
Chọn đáp án A.
Bài 3. Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
A. \(\dfrac{2}{5}\)
B. \(\dfrac{1}{5}\)
C. \(\dfrac{3}{5}\)
D. \(\dfrac{3}{4}\)
Lời giải:
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30-12=18.
Xác suất thực nghiệm xuất hiện mặt S là: \(\dfrac{{18}}{{30}} = \dfrac{3}{5}\)
Chọn đáp án C.
Bài 4. Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
A. 0,15
B. 0,3
C. 0,6
D. 0,36
Lời giải: Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).
Chọn đáp án B.
Xác suất thực nghiệm là một khái niệm quan trọng trong toán học, giúp chúng ta dự đoán khả năng xảy ra của một sự kiện dựa trên kết quả của các thử nghiệm thực tế. Trong chương trình Toán 6 Chân trời sáng tạo, học sinh sẽ được làm quen với khái niệm này thông qua các hoạt động thực hành và ví dụ minh họa.
Xác suất thực nghiệm của một sự kiện A là tỉ số giữa số lần sự kiện A xảy ra và tổng số lần thực hiện thử nghiệm. Công thức tính xác suất thực nghiệm được biểu diễn như sau:
P(A) = (Số lần sự kiện A xảy ra) / (Tổng số lần thực hiện thử nghiệm)
Ví dụ: Gieo một con xúc xắc 6 mặt 100 lần. Nếu mặt 6 xuất hiện 18 lần, thì xác suất thực nghiệm của sự kiện “mặt 6 xuất hiện” là:
P(mặt 6) = 18 / 100 = 0.18
Để tính xác suất thực nghiệm, chúng ta cần thực hiện các bước sau:
Lưu ý: Số lần thực hiện thử nghiệm càng lớn, thì xác suất thực nghiệm càng gần với xác suất lý thuyết.
Ví dụ 1: Một hộp có 10 quả bóng, trong đó có 3 quả bóng màu đỏ, 4 quả bóng màu xanh và 3 quả bóng màu vàng. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất thực nghiệm để lấy được quả bóng màu đỏ sau khi thực hiện 50 lần lấy bóng (có hoàn lại).
Giả sử sau 50 lần lấy bóng, có 16 lần lấy được quả bóng màu đỏ. Khi đó, xác suất thực nghiệm để lấy được quả bóng màu đỏ là:
P(bóng đỏ) = 16 / 50 = 0.32
Ví dụ 2: Tung một đồng xu 20 lần. Nếu mặt ngửa xuất hiện 12 lần, thì xác suất thực nghiệm để tung được mặt ngửa là:
P(mặt ngửa) = 12 / 20 = 0.6
Xác suất thực nghiệm được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Để củng cố kiến thức về Lý thuyết Xác suất thực nghiệm, các em hãy làm các bài tập sau:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Xác suất thực nghiệm Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt!