Phân số là một khái niệm cơ bản trong toán học, được sử dụng để biểu diễn một phần của một tổng thể. Bài viết này sẽ cung cấp một cái nhìn tổng quan về lý thuyết phân số, tập trung vào các phân số có tử số và mẫu số là số nguyên.
Chúng ta sẽ cùng nhau khám phá định nghĩa, các loại phân số, các phép toán cơ bản và các ứng dụng thực tế của phân số trong cuộc sống.
Lý thuyết Phân số với tử số và mẫu số là nguyên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
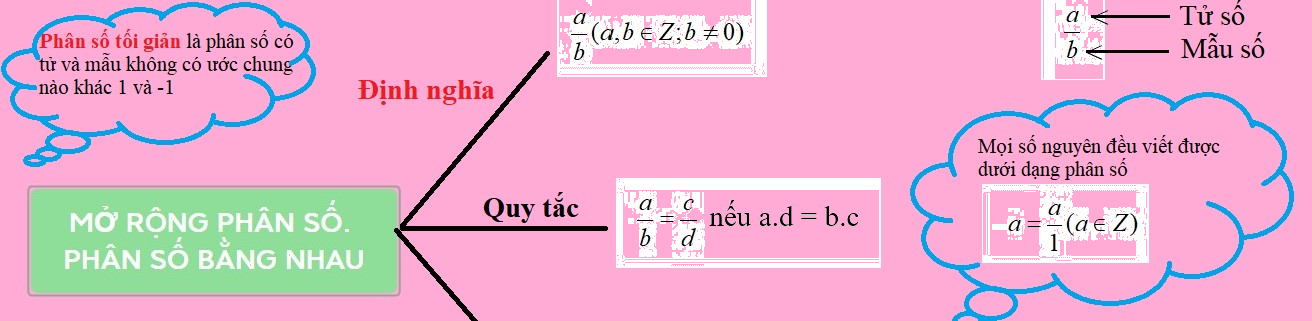
Với \(a,b \in \mathbb{Z},\,b \ne 0\), ta gọi \(\dfrac{a}{b}\) là một phân số, trong đó a là tử số (tử) và b là mẫu số (mẫu) của phân số.
Ví dụ 1:
\(\dfrac{2}{5};\,\dfrac{{ - 3}}{4};\dfrac{{ - 1}}{{ - 7}};...\) là những phân số
Ví dụ 2:
Phân số \(\dfrac{{ - 4}}{7}\) đọc là: Âm bốn phần bảy, có tử số là \( - 4\) và mẫu số là \(7\).
Chú ý:
+ Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu.
+ Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.
a) Khái niệm hai phân số bằng nhau
Hai phân số bằng nhau nếu chúng cùng biểu diễn một giá trị.
b) Quy tắc bằng nhau của hai phân số
Xét hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\)
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\). Ngược lại, nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\)
Ví dụ:
Do \(3.5 = ( - 5).( - 3)\) nên \(\dfrac{3}{{ - 5}} = \dfrac{{ - 3}}{5}\)
Do \(2.\left( { - 3} \right) \ne 5.7\) nên \(\dfrac{2}{5} \ne \dfrac{7}{{ - 3}}\)
Chú ý:
Với \(a,b\) là hai số nguyên và \(b \ne 0\), ta luôn có: \(\dfrac{a}{{ - b}} = \dfrac{{ - a}}{b}\) và \(\dfrac{{ - a}}{{ - b}} = \dfrac{a}{b}\).
Mỗi số nguyên \(n\) có thể coi là phân số \(\dfrac{n}{1}\) (Viết \(\dfrac{n}{1} = n\)). Khi đó số nguyên \(n\) được biểu diễn diễn ở dạng phân số \(\dfrac{n}{1}\).
Ví dụ:
\(\dfrac{{ - 14}}{1} = - 14;\,\,\,\,\,52 = \dfrac{{52}}{1}\).
CÁC DẠNG TOÁN VỀ PHÂN SỐ VỚI TỬ SỐ VÀ MẪU SỐ NGUYÊN
- Sử dụng định nghĩa phân số:
Người ta gọi \(\dfrac{a}{b}\) với \(a,b \in Z;b \ne 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.
- Quan sát hình vẽ hoặc dựa vào các dự kiện đề bài ra để mô tả các bài toán thực tiễn qua phân số. Ý nghĩa tử số và mẫu số của phân số:+) Mẫu số cho biết đơn vị được chia ra làm mấy phần bằng nhau +) Tử số cho biết số phần bằng nhau đã lấy.
Chú ý: Mẫu của phân số phải khác 0.
- Nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\);
- Nếu \(a.d \ne b.c\) thì \(\dfrac{a}{b} \ne \)\(\dfrac{c}{d}\);
\(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) nên \(a.d = b.c\) (định nghĩa hai phân số bằng nhau)
Suy ra \(a = \dfrac{{b.c}}{d}\) , \(d = \dfrac{{b.c}}{a}\) , \(b = \dfrac{{a.d}}{c}\) , \(c = \dfrac{{a.d}}{b}.\)
Từ định nghĩa phân số bằng nhau ta có:
\(a.d = b.c\) \( \Rightarrow \) \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) ;
\(a.d = c.b\) \( \Rightarrow \) \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\) ;
\(d.a = b.c\) \( \Rightarrow \) \(\dfrac{d}{b}\) = \(\dfrac{c}{a}\) ;
\(d.a = c.b\) \( \Rightarrow \) \(\dfrac{d}{c}\) = \(\dfrac{b}{a}\) ;
Phân số là một biểu thức toán học được sử dụng để biểu diễn một phần của một tổng thể. Nó được viết dưới dạng a/b, trong đó a là tử số và b là mẫu số. Cả tử số và mẫu số đều là số nguyên, và mẫu số phải khác 0.
Một phân số a/b được gọi là phân số khi a và b là các số nguyên và b ≠ 0. 'a' được gọi là tử số, biểu thị số phần được chọn. 'b' được gọi là mẫu số, biểu thị tổng số phần bằng nhau trong toàn bộ.
Để cộng hoặc trừ hai phân số, chúng phải có cùng mẫu số. Nếu không, ta cần quy đồng mẫu số trước khi thực hiện phép tính.
Công thức:
a/b + c/b = (a + c)/b
a/b - c/b = (a - c)/b
Ví dụ: 1/2 + 1/2 = 2/2 = 1
Để nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
Công thức:
(a/b) * (c/d) = (a * c) / (b * d)
Ví dụ: (1/2) * (2/3) = 2/6 = 1/3
Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
Công thức:
(a/b) / (c/d) = (a/b) * (d/c) = (a * d) / (b * c)
Ví dụ: (1/2) / (1/3) = (1/2) * (3/1) = 3/2
Có nhiều cách để so sánh phân số:
Phân số được sử dụng rộng rãi trong nhiều lĩnh vực của cuộc sống, bao gồm:
Để củng cố kiến thức về phân số, hãy thực hành giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn toàn diện về lý thuyết phân số với tử số và mẫu số là nguyên. Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng nó vào giải quyết các bài toán thực tế.