Chào mừng các em học sinh đến với bài học về Lý thuyết Số thập phân trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về số thập phân, giúp các em hiểu rõ hơn về cấu trúc và cách sử dụng chúng trong các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng cao, dễ hiểu và phù hợp với từng đối tượng học sinh. Hãy cùng chúng tôi khám phá thế giới số thập phân một cách thú vị và hiệu quả!
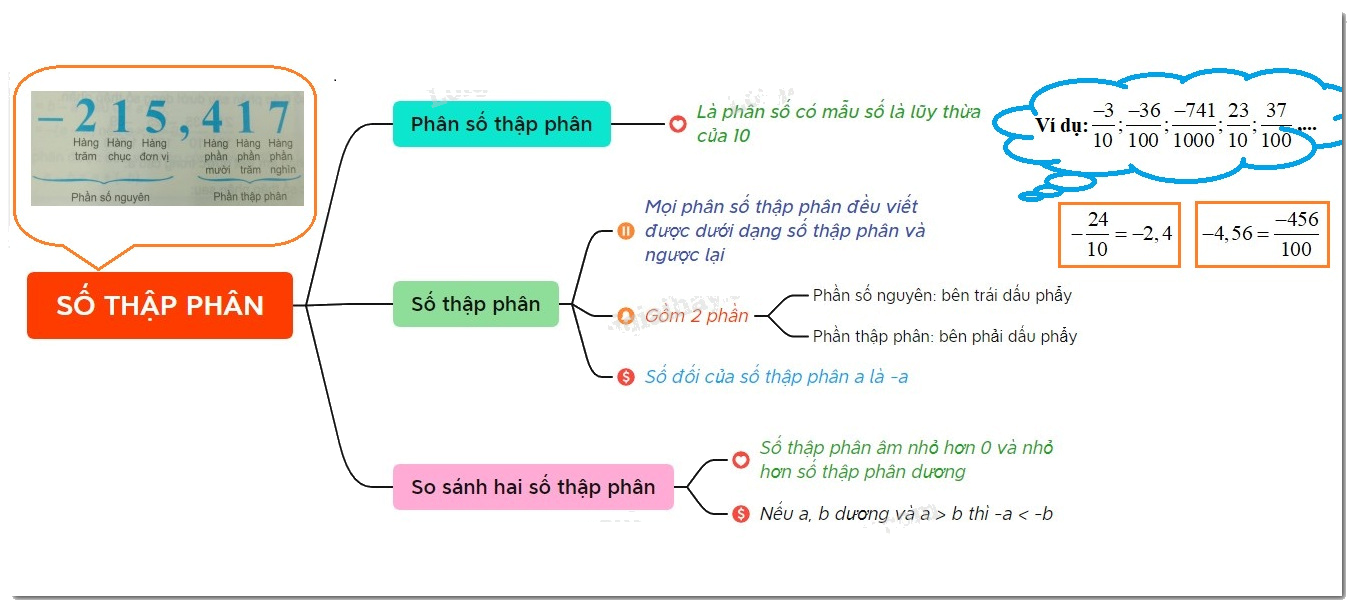
Lý thuyết Số thập phân Toán 6 Chân trời sáng tạo ngắn gọn ,đầy đủ, dễ hiểu
Phân số thập phân là là phân số mà mẫu là lũy thừa của $10$.
Ví dụ:
$\dfrac{7}{{10}};\dfrac{{ - 15}}{{1000}};...$ là các phân số thập phân.
- Ta viết $ - \dfrac{{15}}{{10}} = - 1,5$ và gọi $ - 1,5$ là số thập phân âm, đọc là “ âm một phẩy năm”.
- Các số $2,3;\,\,0,24;...$gọi là các số thập phân dương, đôi khi còn được viết là $ + 2,3;\,\, + 0,24;...$
- Các số thập phân dương và các số thập phân âm gọi chung là số thập phân.
Nhận xét:
- Mọi phân số thập phân đều viết được dưới dạng số thập và ngược lại.
- Số thập phân gồm hai phần:
+ Phần số nguyên viết bên trái dấu phẩy;
+ Phần thập phân viết bên phải dấu phẩy.
- Số thập phân âm nhỏ hơn $0$ và nhỏ hơn số thập phân dương
- Nếu $a,b$ là hai số thập phân dương và $a > b$ thì $ - a < - b$.
Ví dụ:
a) $2,34 < 5,21$
b) Do $2,3 > 1,5$ nên $ - 2,3 < - 1,5$.
Chú ý:
Nếu $a < b$ và $b < c$ thì $a < c$.
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ:
Số đối của $ - 1,5$ là $1,5$.
Số đối của $24,3$ là $ - 24,3$
Số thập phân là một phần quan trọng trong chương trình Toán 6, là nền tảng để học các kiến thức nâng cao hơn ở các lớp trên. Hiểu rõ về số thập phân giúp học sinh giải quyết các bài toán thực tế một cách dễ dàng và chính xác.
Số thập phân là cách biểu diễn các số không nguyên bằng cách sử dụng dấu phẩy (,) để phân tách phần nguyên và phần thập phân. Ví dụ: 3,5; 0,75; 12,01 là các số thập phân.
Một số thập phân có thể được phân tích thành tổng của các phân số thập phân. Ví dụ:
3,5 = 3 + 0,5 = 3 + 5/10
0,75 = 0 + 0,75 = 0 + 75/100
Để so sánh hai số thập phân, ta thực hiện các bước sau:
a. Phép cộng và phép trừ:
Để cộng hoặc trừ hai số thập phân, ta đặt hai số theo cột dọc sao cho các hàng tương ứng thẳng hàng (hàng đơn vị với hàng đơn vị, hàng phần mười với hàng phần mười, ...). Sau đó, ta cộng hoặc trừ các số như cộng hoặc trừ các số tự nhiên.
Ví dụ:
3,5 + 2,7 = 6,2
5,8 - 1,3 = 4,5
b. Phép nhân:
Để nhân hai số thập phân, ta nhân hai số như nhân hai số tự nhiên, sau đó đếm tổng số chữ số ở phần thập phân của hai số. Cuối cùng, ta đặt dấu phẩy vào tích sao cho có số chữ số ở phần thập phân bằng tổng số chữ số ở phần thập phân của hai số.
Ví dụ:
2,5 x 1,2 = 3,00 = 3
c. Phép chia:
Để chia hai số thập phân, ta chuyển cả số bị chia và số chia thành số tự nhiên bằng cách nhân cả hai số với một lũy thừa của 10. Sau đó, ta thực hiện phép chia như chia hai số tự nhiên.
Ví dụ:
7,5 : 0,5 = 75 : 5 = 15
Số thập phân được sử dụng rộng rãi trong cuộc sống hàng ngày, ví dụ như:
Để củng cố kiến thức về số thập phân, các em có thể thực hiện các bài tập sau:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Số thập phân Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt!