Chào mừng các em học sinh đến với bài học về Lý thuyết Số nguyên âm và tập hợp các số nguyên trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về các loại số nguyên, cách biểu diễn chúng trên trục số và các phép toán cơ bản với số nguyên.
Giaitoan.edu.vn tự hào là nền tảng học toán online uy tín, cung cấp nội dung bài giảng chất lượng cao, dễ hiểu và phù hợp với chương trình học của Bộ Giáo dục và Đào tạo.
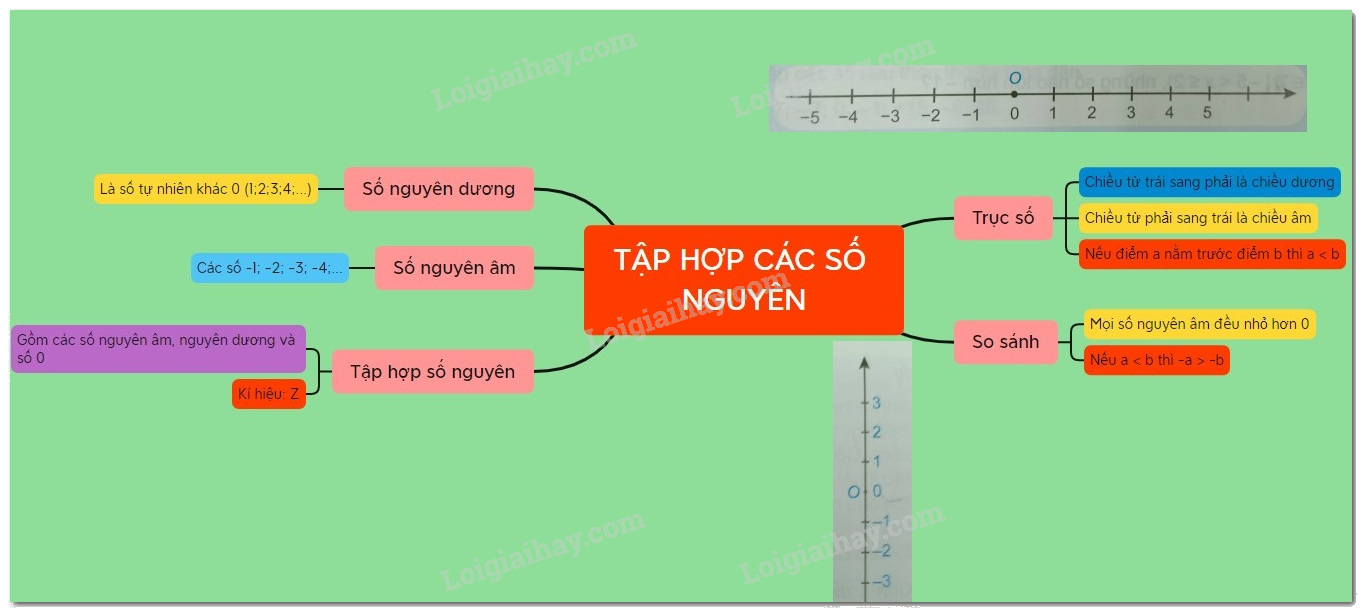
Lý thuyết Số nguyên âm và tập hợp các số nguyên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
I. Số nguyên âm
1. Cách viết và đọc số nguyên âm
Các số tự nhiên \(1,\,\,2,\,\,3,\,\,4,...\)còn được gọi là các số nguyên dương.
Các số \( - 1,\,\, - 2,\,\, - 3,\,...\) gọi là các số nguyên âm đọc là âm một, âm hai, âm ba,… hoặc trừ một, trừ hai, trừ ba,…
Các số nguyên dương \(1,\,\,2,\,\,3,\,...\) đều mang dấu “+” nên còn được viết được viết là \( + 1,\,\, + 2, + 3,...\)
Cách nhận biết số nguyên âm:
Số nguyên âm được nhận biết bằng dấu “ – “ ở trước số tự nhiên khác 0.
Ví dụ:
\( - 5\) là số nguyên âm, đọc là: âm năm hoặc trừ năm
Âm hai được viết là: \( - 2\).
2. Ứng dụng thực tiễn
Số nguyên âm được sử dụng trong nhiều tình huống thực tiễn cuộc sống:
- Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).
- Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
- Số nguyên âm được dùng để chỉ số tiền nợ, cũng như để chỉ số tiền lỗ trong kinh doanh.
- Số nguyên âm được dùng để chỉ thời gian trước Công nguyên.
Ví dụ:
+ Bác An nợ \(100\,\,000\) đồng thì ta cũng có thể nói bác An có \( - 100\,\,000\) đồng.
+ Một cơ sở kinh doanh bị lỗ \(30\,\,000\,\,000\) đồng thì ta có thể nói lợi nhuận là: \( - 30\,\,000\,\,000\) đồng.
+ Nhà toán học Py-ta-go sinh năm \( - 570\), nghĩa là ông sinh năm \(570\) trước Công nguyên
+ Nhiệt độ 3 độ dưới \({0^o}C\) được viết là \( - {3^o}C\); đọc là: âm ba độ C.
+ Vùng đất trũng dưới mực nước biển \(5\,\,m\), ta nói độ cao trung bình của vùng đất đó là \( - 5\,\,m\).
Tập hợp số gồm các số nguyên âm, số \(0\) và các số nguyên dương được gọi là tập hợp số nguyên.
Tập hợp các số nguyên được kí hiệu là \(\mathbb{Z}\).
\(\mathbb{Z} = \left\{ {...;\, - 4;\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4;...} \right\}\)
Chú ý:
Số \(0\) không là số nguyên dương, cũng không là số nguyên âm.
Ví dụ 1:
\(1;\,\,23;\,247;\, - 1;\, - 92;\,- 143\) là các số nguyên.
Ví dụ 2:
Ta có: \( - 3 \in \mathbb{Z};\,\,0 \in \mathbb{Z};\,\,25 \in \mathbb{Z}\).
1. Trục số nằm ngang

- Chiều dương hướng từ trái sang phải, chiều ngược lại là chiều âm.
- Điểm gốc của trục số là điểm \(0\).
- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).
- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).
Ví dụ:

Trên trục số đã cho:
+ Điểm \(A\) biểu diễn số \( - 5\).
+ Điểm \(C\) biểu diễn số \( - 1\).
+ Điểm \(M\) biểu diễn số \(2\).
2. Trục số thẳng đứng
- Chiều dương hướng từ dưới lên trên, chiều ngược lại là chiều âm.
- Điểm gốc của trục số là điểm \(0\).
- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).
- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).
Hai số nguyên trên trục số nằm ở hai phía của điểm \(0\) và cách đều điểm \(0\) được gọi là hai số đối nhau.
Chú ý:
- Số đối của một số nguyên dương là một số nguyên âm.
- Số đối của một số nguyên âm là một số nguyên dương.
- Số đối của \(0\) là \(0.\)
Ví dụ:
+ Số đối của \(3\) là \( - 3\).
+ Số đối của \( - 12\) là \(12\).
+ Số đối của 2021 là \( - 2021\).
CÁC DẠNG TOÁN VỀ SỐ NGUYÊN ÂM VÀ TẬP HỢP CÁC SỐ NGUYÊN
- Cách dùng để diễn tả nhiệt độ
+ Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).
+ Số nguyên dương được dùng để chỉ nhiệt độ trên \({0^o}C\).
- Cách dùng để chỉ độ cao so với mực nước biển
+ Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
+ Số nguyên dương được dùng để chỉ độ cao trên mực nước biển.
- Cách dùng để chỉ số tiền lãi (lỗ), số tiền nợ
+ Số nguyên âm được dùng để chỉ số tiền nợ, cũng như chỉ số tiền lỗ trong kinh doanh
+ Số nguyên dương được dùng để chỉ số tiền lãi trong kinh doanh.
- Cách dùng để chỉ thời gian trước và sau công nguyên
+ Số nguyên âm được dùng để chỉ thời gian trước công nguyên.
+ Số nguyên dương được dùng để chỉ thời gian sau công nguyên.
Phương pháp: Sử dụng định nghĩa các tập hợp số sau đây:
- Tập hợp số tự nhiên: \(\mathbb{N} = \left\{ {0;\,1;\,2;\,3;....} \right\}\)
- Tập hợp số tự nhiên khác 0: \({\mathbb{N}^*} = \left\{ {1;\,2;\,3;\,....} \right\}\)
- Tập hợp số nguyên: \(\mathbb{Z} = \left\{ {...; - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\)
+ Các số nguyên âm: \( - 1;\, - 2;\, - 3;\, - 4;...\)
+ Các số nguyên dương: \(1;\,2;\,3;\,4;\,...\)
Chú ý: Số 0 không là số nguyên âm cũng không là số nguyên dương.
- Trên trục số nằm ngang:
+ Các điểm biểu diễn số nguyên âm nằm ở bên trái gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên phải gốc 0.
- Trên trục số thẳng đứng:
+ Các điểm biểu diễn số nguyên âm nằm ở bên dưới gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên trên gốc 0.
Phương pháp:
- Hai số đối nhau chỉ khác nhau về dấu.
- Số đối của $0$ là $0.$
Ví dụ:
Tìm số đối của \( - 7\)?
Ta thấy số -7 mang dấu “-“ nên số đối của nó sẽ mang dấu “+”
Vì vậy số đối của \( - 7\) là 7.
Trong chương trình Toán 6, việc nắm vững kiến thức về số nguyên âm và tập hợp các số nguyên là nền tảng quan trọng để học tốt các kiến thức toán học ở các lớp trên. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, giúp các em học sinh hiểu rõ hơn về các khái niệm và ứng dụng của chúng.
Số nguyên âm là các số thực nhỏ hơn 0. Chúng được biểu diễn bằng dấu trừ (-) phía trước số. Ví dụ: -1, -2, -3, -10, -100,... Số nguyên âm thường được sử dụng để biểu diễn các đại lượng có tính chất ngược lại, như nợ, nhiệt độ dưới 0 độ C, độ sâu dưới mực nước biển,...
Số nguyên dương là các số thực lớn hơn 0. Chúng được biểu diễn không có dấu hoặc có dấu cộng (+) phía trước số. Ví dụ: 1, 2, 3, 10, 100,... Số nguyên dương thường được sử dụng để biểu diễn các đại lượng có tính chất thuận, như tuổi, số lượng, chiều cao,...
Số 0 là số nguyên không âm cũng không dương. Nó là điểm trung gian giữa các số nguyên âm và số nguyên dương. Số 0 có vai trò quan trọng trong các phép toán số học, như cộng, trừ, nhân, chia.
Tập hợp các số nguyên (ký hiệu là ℤ) bao gồm tất cả các số nguyên âm, số nguyên dương và số 0. Tập hợp này được biểu diễn bằng công thức: ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Trục số là một đường thẳng, trên đó ta chọn một điểm làm gốc (thường là số 0). Các số nguyên dương được biểu diễn ở phía bên phải gốc, các số nguyên âm được biểu diễn ở phía bên trái gốc. Khoảng cách từ một số nguyên đến gốc trên trục số được gọi là giá trị tuyệt đối của số nguyên đó.
Để so sánh hai số nguyên, ta thực hiện theo các quy tắc sau:
Các phép toán cộng, trừ, nhân, chia với số nguyên được thực hiện theo các quy tắc sau:
Để củng cố kiến thức về lý thuyết số nguyên âm và tập hợp các số nguyên, các em có thể thực hiện các bài tập sau:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và quan trọng về lý thuyết số nguyên âm và tập hợp các số nguyên Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt!