Chào mừng các em học sinh đến với bài học về Lý thuyết Hình có trục đối xứng trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ giúp các em hiểu rõ khái niệm về trục đối xứng, cách nhận biết hình có trục đối xứng và ứng dụng của nó trong thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để các em có thể nắm vững kiến thức một cách hiệu quả nhất.
Lý thuyết Hình có trục đối xứng Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
I. Thế nào là một hình có trục đối xứng
Các hình có tính chất:
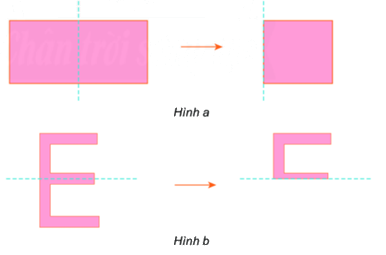
Ta nhận thấy khi gấp theo đường nét đứt hai phần của mỗi hình chồng khít lên nhau.
Hai hình trên là hình có trục đối xứng.
Đường nét đứt ở mỗi hình trên là trục đối xứng của hình đó.
Ví dụ: Các hình sau là các hình có trục đối xứng
1.
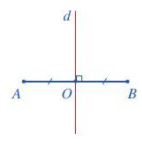
Đoạn thẳng AB là hình có trục đối xứng và trục đối xứng là đường thẳng d đi qua trung
điểm 0 của đoạn thẳng AB và vuông góc với AB.
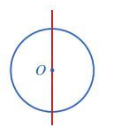
2.
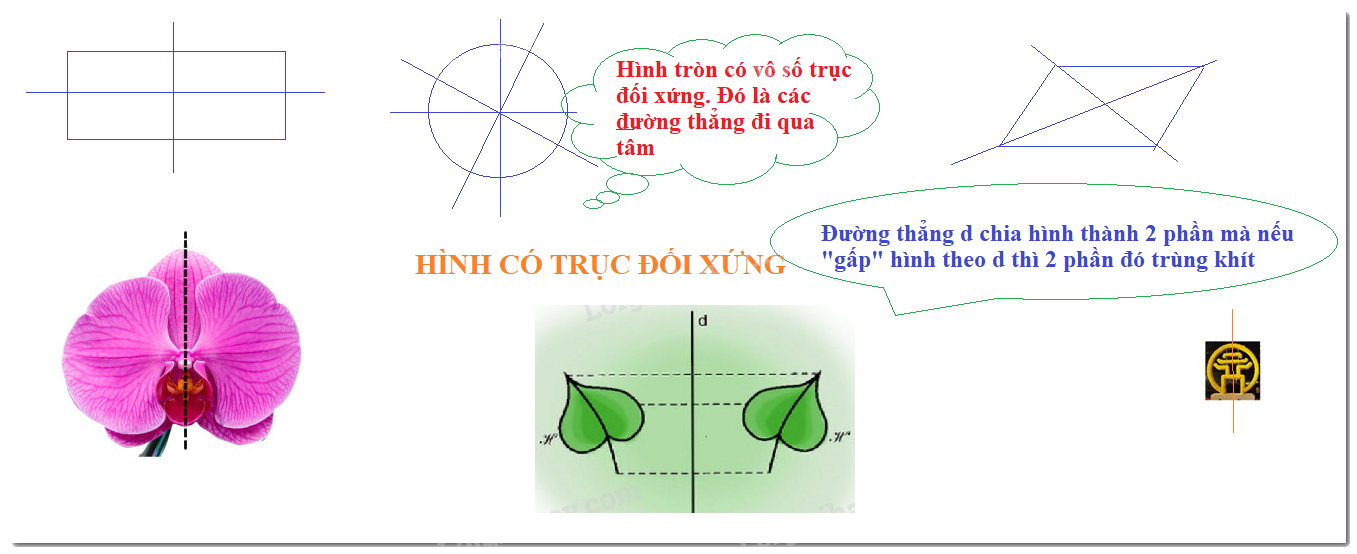
Đường tròn là hình có nhiều trục đối xứng và mỗi trục đối xứng là một đường thẳng đi tâm của nó
3.
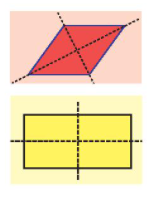
Mỗi đường chéo là một trục đối xứng của hình thoi.
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
4.
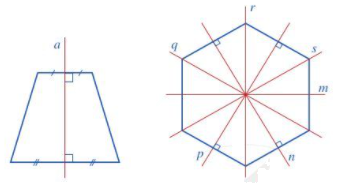
Hình thang cân có 1 trục đối xứng là đường thẳng a
Hình lục giác đều có 6 trục đối xứng là các đường thẳng m, n, p, q, r, s.
III. Nhận biết những hình phẳng trong tự nhiên có trục đối xứng
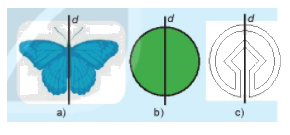
Thế giới tự nhiên rất phong phú và đa dạng, nhiều hình ảnh trong chúng có trục đối xứng.
Chẳng hạn con chuồn chuồn ở hình a), chiếc lá ở hình b) là những hình có trục đối xứng; quả chuối ở hình c) không có trục đối xứng.



Trong chương trình Toán 6 Chân trời sáng tạo, kiến thức về hình học đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng quan sát của học sinh. Một trong những khái niệm cơ bản và thú vị nhất là Hình có trục đối xứng. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết này, giúp các em học sinh hiểu rõ và áp dụng vào giải các bài tập một cách hiệu quả.
Định nghĩa: Trục đối xứng của một hình là đường thẳng sao cho nếu gấp hình theo đường thẳng đó thì hai phần của hình trùng khít lên nhau.
Ví dụ: Hình chữ nhật có hai trục đối xứng là hai đường thẳng đi qua trung điểm các cạnh đối diện. Hình vuông có bốn trục đối xứng.
Để nhận biết một hình có trục đối xứng, ta có thể thực hiện các bước sau:
Ngoài ra, ta cũng có thể sử dụng tính chất đối xứng để nhận biết trục đối xứng. Nếu một hình có tính chất đối xứng qua một đường thẳng, thì đường thẳng đó là trục đối xứng của hình.
Hình có trục đối xứng xuất hiện rất nhiều trong thực tế, từ các công trình kiến trúc, đồ vật hàng ngày đến các hình ảnh trong tự nhiên. Ví dụ:
Bài 1: Hình nào sau đây có trục đối xứng?
Bài 2: Vẽ hình vuông ABCD và chỉ ra các trục đối xứng của nó.
Ngoài khái niệm về trục đối xứng, các em có thể tìm hiểu thêm về đối xứng tâm, đối xứng qua một điểm. Đây là những kiến thức quan trọng trong chương trình hình học lớp 6 và các lớp trên.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Hình có trục đối xứng Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!
| Hình | Số trục đối xứng |
|---|---|
| Hình vuông | 4 |
| Hình chữ nhật | 2 |
| Hình thoi | 2 |
| Hình thang cân | 1 |
| Bảng tổng hợp số trục đối xứng của một số hình | |