Chào mừng các em học sinh đến với bài học về Lý thuyết Tập hợp và Phần tử của tập hợp trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về tập hợp, giúp các em làm quen với một khái niệm nền tảng trong toán học.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho các em những bài giảng chất lượng, dễ hiểu và nhiều bài tập thực hành để các em có thể nắm vững kiến thức một cách hiệu quả nhất.
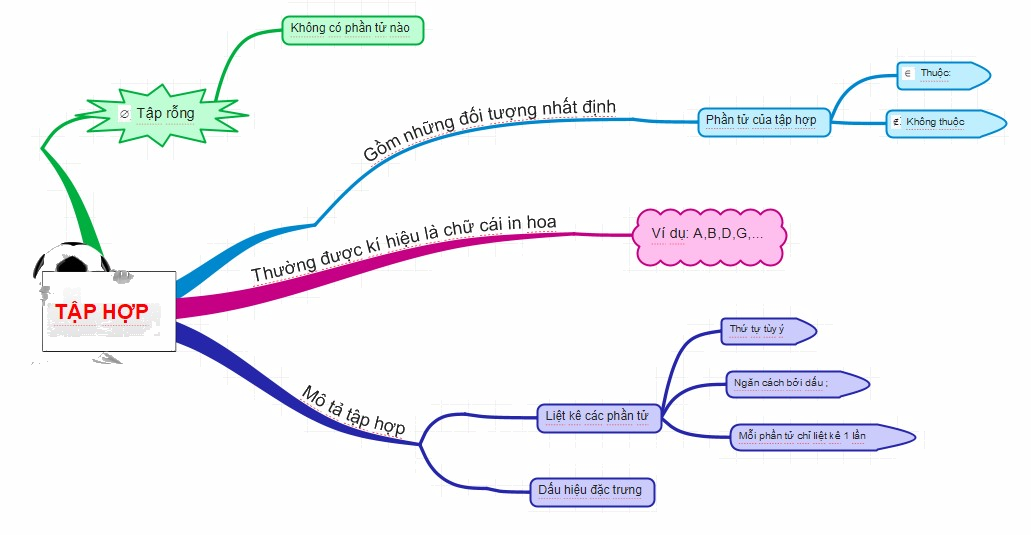
Lý thuyết Tập hợp. Phần tử của tập hợp Toán 6 Chân trời sáng tạo ngắn gọn , đầy đủ, dễ hiểu
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
+ Ví dụ:
a) Tập hợp các bạn nữ trong lớp 6A bao gồm tất cả các bạn nữ của lớp 6A. Đối tượng của tập hợp này là các bạn nữ của lớp 6A. Mỗi một bạn là một phần tử.
b) Tập hợp các số nhỏ hơn gồm tất cả các số nhỏ hơn 6, đó là 0,1,2,3,4,5. Mỗi một số trong 6 số này là một phần tử của tập hợp, chẳng hạn số 0 là một phần tử, số 1 cũng là một phần tử.
+) Ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D,...
+) Sử dụng các chữ cái thường a,b,c,... để kí hiệu cho phần tử.
+) Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,” hoặc dấu “;”(đối với trường hợp là các phần tử số).
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
+) Phần tử \(x\) thuộc tập hợp \(A\) được kí hiệu là \(x \in A\), đọc là “x thuộc A”. Phần tử \(y\) không thuộc tập hợp \(A\) được kí hiệu là \(y \notin A\), đọc là “y không thuộc A”.
Ví dụ: Tập hợp B gồm tất cả các số nhỏ hơn 5
Kí hiệu: \(B = \left\{ {0;1;2;3;4} \right\} = \left\{ {2;1;0;3;4} \right\}\). Mỗi số 0;1;2;3;4 đều là một phần tử của tập hợp B. Số 6 không là phần tử của B( 8 không thuộc B)
Ta viết \(0 \in B;1 \in B;2 \in B;\)\(3 \in B;4 \in B\) và \(8 \notin B\)
Ta không được viết \(B = \left\{ {0;\underline {1;1} ;2;3;4} \right\}\) cách viết này có hai số 1 là cách viết sai.
1. Các cách cho một tập hợp
Cách 1: Liệt kê các phần tử của tập hợp
Kí hiệu: \(B = \left\{ {0;1;2;3;4} \right\} = \left\{ {2;1;0;3;4} \right\}\)
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).
Ví dụ:
a) Tập hợp B gồm tất cả các số nhỏ hơn 5
Liệt kê: \(B = \left\{ {0;1;2;3;4} \right\} = \left\{ {2;1;0;3;4} \right\}\)
Chỉ ra tính chất đặc trưng: \(B = \{ x|x < 5\} \)
b) Tập hợp các số nhỏ hơn 6
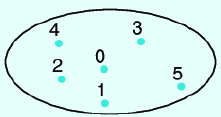
Liệt kê: \(A = \left\{ {0;1;2;3;4;5} \right\}\)
Chỉ ra tính chất đặc trưng: \(B = \{ x|x < 6\} \)
Sơ đồ Venn:
2. Tập rỗng
Tập rỗng là tập hợp không có phần tử nào, kí hiệu \(\emptyset \).
Ví dụ:
Trong toán học, tập hợp là một khái niệm cơ bản và quan trọng. Nó được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ đại số, hình học đến xác suất thống kê. Bài viết này sẽ trình bày chi tiết về lý thuyết tập hợp và phần tử của tập hợp, dành cho học sinh lớp 6 chương trình Chân trời sáng tạo.
Tập hợp là một khái niệm dùng để chỉ một nhóm các đối tượng xác định, được gọi là các phần tử của tập hợp. Các phần tử có thể là bất kỳ đối tượng nào, chẳng hạn như số, chữ cái, người, đồ vật, hoặc thậm chí là các tập hợp khác.
Ví dụ:
Phần tử là một đối tượng thuộc về một tập hợp. Ký hiệu để chỉ một phần tử thuộc tập hợp A là '∈'. Nếu một đối tượng không thuộc tập hợp A, ta ký hiệu là '∉'.
Ví dụ:
Có hai cách chính để biểu diễn một tập hợp:
Để so sánh hai tập hợp A và B, ta có thể sử dụng các khái niệm sau:
Các phép toán cơ bản trên tập hợp bao gồm:
Hãy thực hành với các bài tập sau để củng cố kiến thức về lý thuyết tập hợp:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và hữu ích về lý thuyết tập hợp và phần tử của tập hợp. Chúc các em học tập tốt!