Chào mừng bạn đến với bài học lý thuyết Góc Toán 6 Chân trời sáng tạo tại giaitoan.edu.vn. Đây là một trong những kiến thức cơ bản và quan trọng nhất trong chương trình Toán 6, giúp các em học sinh xây dựng nền tảng vững chắc cho các bài học tiếp theo.
Chúng tôi cung cấp bài giảng chi tiết, dễ hiểu, kèm theo các ví dụ minh họa sinh động và bài tập thực hành đa dạng để giúp các em nắm vững kiến thức một cách hiệu quả nhất.
Lý thuyết Góc Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Bài 6. Góc
1. Góc
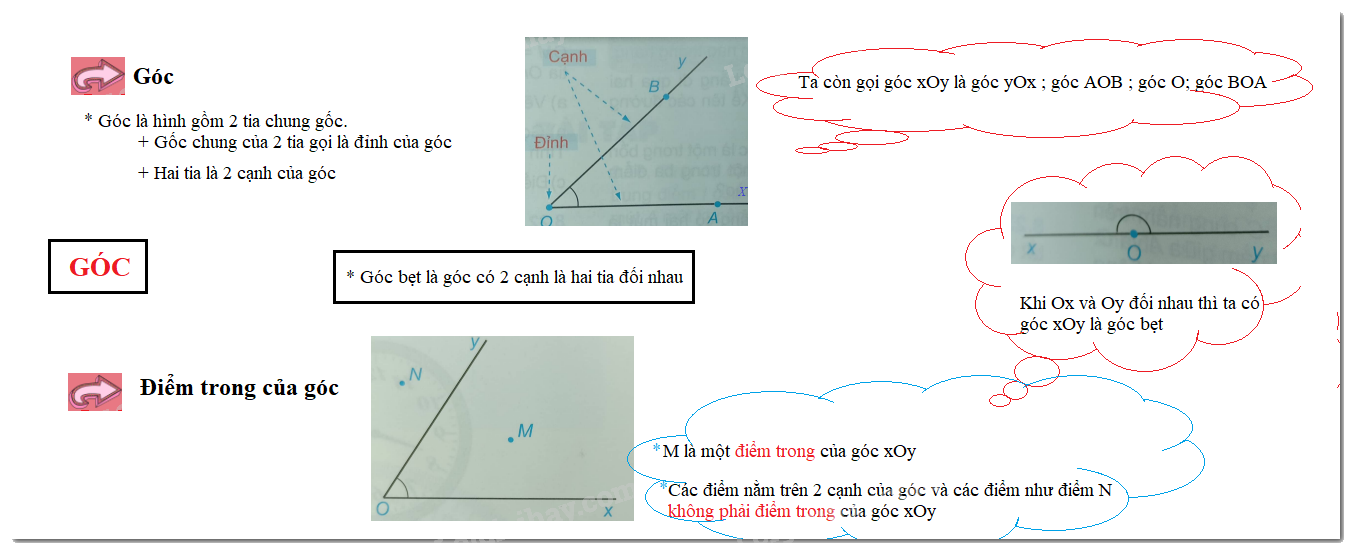
Góc là hình tạo bởi hai tia chung gốc. Gốc chung gọi là đỉnh của góc, hai tia gọi là hai cạnh của góc.
Chú ý: Trong trường hợp nhiều góc có chung một đỉnh, người ta thường khoanh một cung giữa hai cạnh của góc và đánh số: 1, 2, 3, ... hoặc mỗi góc có khoanh những cung khác nhau để chỉ các góc khác nhau đó.
2. Cách vẽ góc
Để vẽ \(\widehat {xOy}\), ta vẽ điểm O trên giấy hoặc bảng, từ điểm O vẽ hai tia Ox và Oy. Ta được \(\widehat {xOy}\).
3. Góc bẹt
Xoay hai cạnh của chiếc compa để hai cạnh đó nằm trên một đường thẳng.
4. Điểm trong của góc
Cho góc xOy khác góc bẹt. Điểm M được gọi là điểm trong của góc xOy không bẹt nếu tia OM cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó.
Góc là một khái niệm cơ bản trong hình học, xuất hiện xuyên suốt trong chương trình Toán học từ cấp tiểu học đến trung học phổ thông. Hiểu rõ lý thuyết về góc là điều kiện cần thiết để giải quyết các bài toán liên quan đến hình học, đặc biệt là trong chương trình Toán 6 Chân trời sáng tạo.
Góc được tạo bởi hai tia chung gốc. Tia chung gốc gọi là cạnh của góc, còn điểm chung gốc gọi là đỉnh của góc. Để xác định một góc, ta thường dùng ký hiệu ∠ (đọc là “góc”) kèm theo tên đỉnh và tên hai cạnh tạo nên góc. Ví dụ: ∠ABC là góc có đỉnh B và hai cạnh là BA và BC.
Trong hình học, có nhiều loại góc khác nhau dựa trên số đo của chúng:
Có nhiều cách để đặt tên cho một góc:
Để so sánh hai góc, ta sử dụng số đo của chúng. Góc nào có số đo lớn hơn thì góc đó lớn hơn.
Ví dụ: Nếu ∠A = 60° và ∠B = 90°, thì ∠A < ∠B.
Tổng hai góc là tổng số đo của hai góc đó. Ví dụ: Nếu ∠A = 30° và ∠B = 45°, thì ∠A + ∠B = 75°.
Hai góc kề bù là hai góc có chung cạnh, không có điểm chung bên trong và tổng số đo bằng 180°. Ví dụ: ∠A và ∠B là hai góc kề bù nếu chúng có chung cạnh AB và ∠A + ∠B = 180°.
Hai góc kề nhau là hai góc có chung cạnh và không có điểm chung bên trong. Ví dụ: ∠A và ∠B là hai góc kề nhau nếu chúng có chung cạnh AB và không có điểm chung bên trong.
Bài 1: Cho ∠ABC = 50°. Tính số đo của góc kề bù với ∠ABC.
Giải: Vì ∠ABC và ∠ABD là hai góc kề bù nên ∠ABC + ∠ABD = 180°. Suy ra ∠ABD = 180° - ∠ABC = 180° - 50° = 130°.
Bài 2: Vẽ ∠MNP = 75° bằng thước và compa.
Giải: (Hướng dẫn chi tiết cách vẽ góc bằng thước và compa)
Lý thuyết về góc có ứng dụng rộng rãi trong thực tế, từ việc thiết kế kiến trúc, xây dựng công trình đến việc đo đạc, định vị trong hàng hải, hàng không. Ví dụ, các kiến trúc sư sử dụng lý thuyết góc để thiết kế các tòa nhà có tính thẩm mỹ cao và đảm bảo độ vững chắc. Các kỹ sư sử dụng lý thuyết góc để tính toán các góc độ trong các công trình xây dựng.
Để nắm vững kiến thức về lý thuyết góc, các em học sinh nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Hy vọng bài học này sẽ giúp các em hiểu rõ hơn về lý thuyết Góc Toán 6 Chân trời sáng tạo. Chúc các em học tập tốt!