Chương 3 trong chương trình Toán học thường tập trung vào một chủ đề quan trọng, đòi hỏi sự nắm vững kiến thức nền tảng.
Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống lý thuyết ôn tập chương 3 được trình bày một cách rõ ràng, dễ hiểu, giúp bạn củng cố kiến thức và tự tin hơn trong quá trình học tập.
Hãy cùng khám phá những kiến thức cốt lõi và phương pháp giải bài tập hiệu quả ngay sau đây!
Lý thuyết ôn tập chương 3
I. Hình thoi
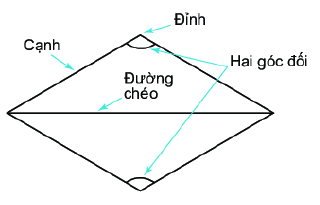
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau:
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
Chu vi hình thoi cạnh a bằng độ dài cạnh nhân với bốn: \(C = 4a\)
Diện tích hình thoi cạnh a bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
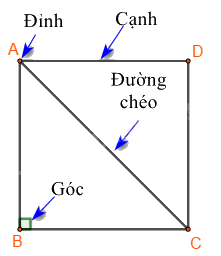
Bốn cạnh bằng nhau: \(AB = BC = CD = DA; \)
Hai cạnh đối \(AB \) và \(CD; \) \(AD \) và \(BC \) song song với nhau;
Hai đường chéo bằng nhau: \(AC = BD; \)
Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D \) là góc vuông.
Chu vi hình vuông cạnh a là: \(C = 4a\)
Diện tích hình vuông cạnh a là: \(S = a.a = {a^2}\).
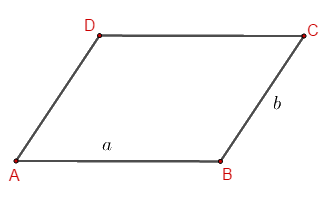
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).
- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.
Chu vi hình bình hành : \(C = 2(a + b)\).
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
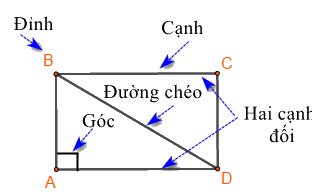
Hình chữ nhật \(ABCD\) có:
- Bốn đỉnh A, B, C, D
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,\,BC = AD\).
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Chu vi của hình chữ nhật là: \(C = 2\left( {a + b} \right);\)
Diện tích của hình chữ nhật là: \(S = a.b\)
Trong đó a, b là chiều dài và chiều rộng của HCN.
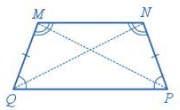
Hình thang cân \(MNPQ\) có:
Hai cạnh cạnh bên song song: \(MN\) song song với \(PQ\).
- Hai cạnh bên bằng nhau: \(MQ = NP\).
- Hai đường chéo bằng nhau: \(MP = NQ\).
- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau.
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
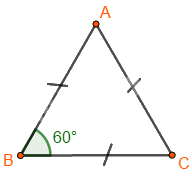
Tam giác đều \(ABC\) có:
+ Ba cạnh bằng nhau: \(AB = BC = CA\).
+ Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.
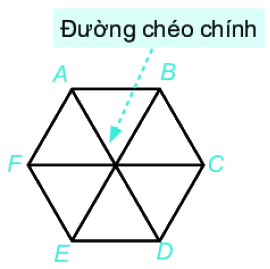
Lục giác đều \(ABCDEF\) có:
- Sáu đỉnh A, B, C, D, E, F
- Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).
- Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau \(AD = BE = CF\).
Chương 3 trong chương trình Toán học thường xoay quanh một chủ đề cụ thể, ví dụ như các phép biến đổi đại số, phương trình bậc hai, hệ phương trình, hoặc các khái niệm hình học như tam giác đồng dạng, đường tròn. Việc nắm vững lý thuyết là nền tảng quan trọng để giải quyết các bài tập một cách chính xác và hiệu quả.
Để bắt đầu ôn tập chương 3, chúng ta cần xác định rõ các khái niệm trọng tâm. Ví dụ, nếu chương 3 nói về phương trình bậc hai, các khái niệm như nghiệm của phương trình, biệt thức delta, và các công thức nghiệm cần được hiểu rõ.
Ngoài các khái niệm, chương 3 cũng thường chứa các định lý và tính chất quan trọng. Việc hiểu rõ các định lý này sẽ giúp bạn giải quyết các bài tập phức tạp một cách dễ dàng hơn. Ví dụ, trong hình học, các định lý về tam giác đồng dạng, đường tròn, hoặc các tính chất của hình vuông, hình chữ nhật là những kiến thức không thể bỏ qua.
Chương 3 thường xuất hiện nhiều dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Dưới đây là một số dạng bài tập thường gặp:
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh áp dụng trực tiếp các công thức đã học để giải quyết bài toán. Ví dụ, tính nghiệm của phương trình bậc hai, tính độ dài cạnh của tam giác vuông, hoặc tính diện tích hình tròn.
Dạng bài tập này yêu cầu học sinh chứng minh một đẳng thức, một định lý, hoặc một tính chất nào đó. Để giải quyết dạng bài tập này, bạn cần nắm vững các kiến thức nền tảng và sử dụng các phương pháp chứng minh phù hợp.
Đây là dạng bài tập khó nhất, yêu cầu học sinh kết hợp nhiều kiến thức khác nhau để giải quyết bài toán. Ví dụ, giải một bài toán liên quan đến phương trình bậc hai và hình học, hoặc chứng minh một định lý sử dụng nhiều kiến thức khác nhau.
Để ôn tập chương 3 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ 1: Giải phương trình bậc hai x2 - 5x + 6 = 0.
Giải:
Biệt thức delta = (-5)2 - 4 * 1 * 6 = 25 - 24 = 1.
Vì delta > 0, phương trình có hai nghiệm phân biệt:
x1 = (5 + √1) / 2 = 3
x2 = (5 - √1) / 2 = 2
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Giải:
Áp dụng định lý Pitago, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25.
Vậy BC = √25 = 5cm.
Lý thuyết ôn tập chương 3 là một phần quan trọng trong chương trình Toán học. Việc nắm vững kiến thức và rèn luyện kỹ năng giải bài tập sẽ giúp bạn đạt kết quả tốt trong các kỳ thi. Hãy dành thời gian ôn tập kỹ lưỡng và áp dụng các phương pháp học tập hiệu quả để đạt được mục tiêu của mình.