Chào mừng bạn đến với bài học về Lý thuyết Tập hợp số tự nhiên dành cho học sinh Toán 6 Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về số tự nhiên và cách biểu diễn chúng trong các tập hợp.
Chúng ta sẽ cùng nhau khám phá khái niệm về số tự nhiên, các phép toán cơ bản trên số tự nhiên, và cách sử dụng tập hợp để tổ chức và phân loại các số một cách hiệu quả.
Lý thuyết Tập hợp số tự nhiên. Ghi số tự nhiên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Các số \(0,1,2,3,4,...\) là các số tự nhiên
Tập hợp các số tự nhiên được kí hiệu là \(\mathbb{N}\), tức là \(\mathbb{N} = \left\{ {0;1;2;3;...} \right\}\)
Tập hợp các số tự nhiên khác 0 được kí hiệu là \({\mathbb{N}^*}\), tức là \({\mathbb{N}^*} = \left\{ {1;2;3;...} \right\}\)
Tập hợp \(\mathbb{N}\) bỏ đi số 0 thì được \({\mathbb{N}^*}\).
Khi cho một số tự nhiên \(x \in {\mathbb{N}^*}\) thì ta hiểu \(x\) là số tự nhiên khác 0.
Ví dụ:
Viết tập hợp sau bằng cách liệt kê các phần tử: \(A = \left\{ {a \in {\mathbb{N}^*}\left| {a < 4} \right.} \right\}\)
\(a \in {\mathbb{N}^*}\) nên \(a\) là các số từ 1;2;3;4;5;6;...
Tuy nhiên thêm điều kiện \(a < 4\) nên \(a\) là các số 1;2;3.
Vậy \(A = \left\{ {1;2;3} \right\}\)
a) Biểu diễn các số tự nhiên trên tia số:
Các số tự nhiên được biểu diễn trên tia số như sau:
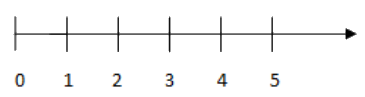
+ Tia số có mũi tên sang phải biểu thị chiều tăng dần của các số tự nhiên.
+ Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n được gọi là điểm n.
+ Điểm 0 được gọi là gốc.
b) So sánh hai số tự nhiên
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết \(a < b\) ( đọc là \(a\) nhỏ hơn \(b\)) hoặc \(b > a.\) (đọc là \(b\) lớn hơn \(a\))
+ Khi biểu diễn trên tia số nằm ngang có chiều từ trái sang phải, nếu \(a < b\) thì điểm \(a\) nằm bên trái điểm \(b\).
Ngoài ra ta cũng viết \(a \ge b\) để chỉ \(a > b\) hoặc \(a = b.\)
+ Nếu \(a < b\) và \(b < c\) thì \(a < c.\) (Tính chất bắc cầu)
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.
+ Số 0 là số tự nhiên bé nhất.
Ví dụ:
a) Số 3 và số 4 là hai số tự nhiên liên tiếp.
b) Số liền sau của 89 là 90.
c) Số liền trước của 16 là 15.
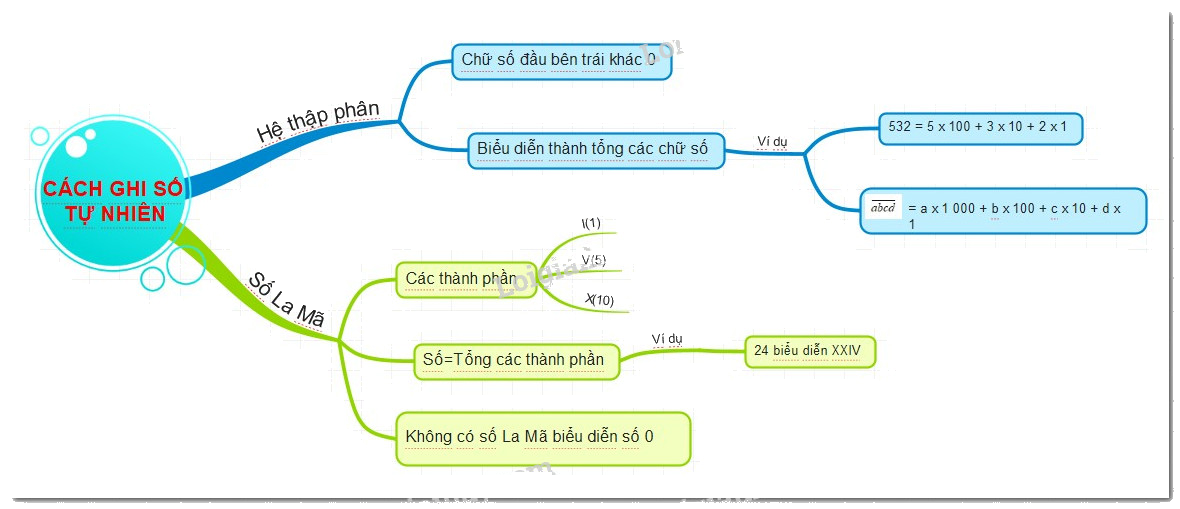
a) Cách ghi số tự nhiên trong hệ thập phân
Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là \(0;1;2;3;4;5;6;7;8;9.\) Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.
Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó. Ví dụ 10 chục thì bằng 1 trăm; mười trăm thì bằng 1 nghìn;...
Chú ý: Khi viết các số tự nhiên, ta quy ước:
1. Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.
2. Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.
3. Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau
b) Hệ thập phân
Ta đã biết cấu tạo thập phân của một số:
- Kí hiệu \(\overline {ab} \) chỉ số tự nhiên có hai chữ số, chữ số hàng chục là \(a\left( {a \ne 0} \right)\), chữ số hàng đơn vị là b. Ta có:
\(\overline {ab} = a \times 10 + b.\)
Kí hiệu \(\overline {abc} \) chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là \(a\left( {a \ne 0} \right)\), chữ số hàng chục là b, chữ số hàng đơn vị là c. Ta có:
\(\overline {abc} = a \times 100 + b \times 10 + c.\)
- Với các số cụ thể thì không viết dẫu gạch ngang ở trên.
Ví dụ:
\(\begin{array}{l}\overline {2b} = 2.10 + b\\\overline {a5b} = a.100 + 5.10 + b\left( {a \ne 0} \right)\end{array}\)
\(\overline {a03bcd} = a.100000 + 0.10000\)\( + 3.1000 + b.100 + c.10 + d\)\(\left( {a \ne 0} \right)\)
c) Hệ La Mã
Cách ghi số La Mã như sau:
Chữ số | I | V | X |
Giá trị tương ứng trong hệ thập phân | 1 | 5 | 10 |
Bảng chuyển đổi số La Mã sang số trong hệ thập phân tương ứng (từ 1 đến 10)
Số La Mã | I | II | III | IV | V | VI | VII | VIII | IX | X |
Giá trị tương ứng trong hệ thập phân | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
XI | XII | XIII | XIV | XV | XVI | XVII | XVIII | XIX | XX |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
XXI | XXII | XXIII | XXIV | XXV | XXVI | XXVII | XXVIII | XXIX | XXX |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số tự nhiên là nền tảng của toán học, và việc nắm vững lý thuyết về tập hợp số tự nhiên là vô cùng quan trọng đối với học sinh lớp 6. Bài viết này sẽ cung cấp một cái nhìn toàn diện về chủ đề này, bao gồm định nghĩa, tính chất, và các ứng dụng thực tế.
Số tự nhiên là các số dùng để đếm. Tập hợp số tự nhiên được ký hiệu là N và bao gồm các số 0, 1, 2, 3, ... Số tự nhiên không bao gồm số âm, số thập phân, hay số phân số.
Các phép toán cơ bản trên số tự nhiên bao gồm:
Tập hợp là một khái niệm quan trọng trong toán học, dùng để nhóm các đối tượng có chung một tính chất nào đó. Tập hợp số tự nhiên N là tập hợp bao gồm tất cả các số tự nhiên.
Số tự nhiên được ghi bằng các chữ số từ 0 đến 9. Ví dụ: 123, 4567, 890.
Trong tập hợp số tự nhiên, có một số tập hợp con quan trọng:
Trục số là một đường thẳng, trên đó ta có thể biểu diễn các số tự nhiên. Điểm 0 là gốc của trục số, và các số tự nhiên được biểu diễn bằng các điểm trên trục số, cách gốc một khoảng bằng giá trị của số đó.
Lý thuyết tập hợp số tự nhiên có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về lý thuyết tập hợp số tự nhiên, bạn có thể thực hành các bài tập sau:
Lý thuyết tập hợp số tự nhiên là một phần quan trọng của chương trình Toán 6. Việc nắm vững kiến thức này sẽ giúp bạn xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn trong tương lai. Hãy luyện tập thường xuyên để hiểu rõ hơn về các khái niệm và ứng dụng của lý thuyết này.