Chào mừng các em học sinh đến với bài học lý thuyết về Hình vuông, Tam giác đều và Lục giác đều trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về các hình đa giác này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, cách vẽ và các ứng dụng thực tế của từng hình. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Lý thuyết Hình vuông- Tam giác đều- Lục giác đều Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
I. Hình vuông
1.Nhận biết hình vuông
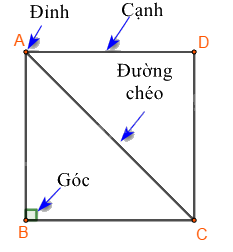
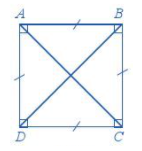
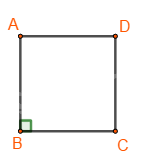
Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\)
Hai cạnh đối \(AB\) và \(CD;\) \(AD\) và \(BC\) song song với nhau;
Hai đường chéo bằng nhau: \(AC = BD;\)
Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\) là góc vuông.
2. Vẽ hình vuông
Vẽ bằng ê ke hình vuông \(ABCD\), biết độ dài cạnh bằng \(a{\rm{ }}cm\).
Bước 1: Vẽ đoạn thẳng \(AB = a\left( {cm} \right)\)
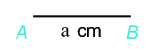
Bước 2: Vẽ đường thẳng vuông góc với \(AB\) tại \(A\). Xác định điểm \(D\) trên đường thẳng đó sao cho \(AD = a\left( {cm} \right)\).
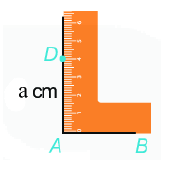
Bước 3: Vẽ đường thẳng vuông góc với \(AB\) tại \(B\). Xác định điểm \(C\) trên đường thẳng đó sao cho \(BC = a\left( {cm} \right)\).
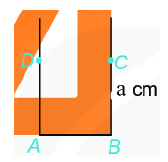
Bước 4: Nối \(C\) với \(D\) ta được hình vuông \(ABCD\).
1. Nhận biết tam giác đều
Trong tam giác đều:
+ Ba cạnh bằng nhau
+ Ba góc bằng nhau.
Ví dụ:
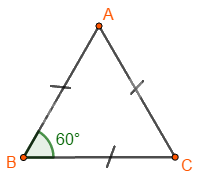
Tam giác đều \(ABC\) có:
+ Ba cạnh bằng nhau: \(AB = BC = CA\).
+ Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.
2. Vẽ tam giác đều
Cách vẽ tam giác đều cạnh \(a\,(cm)\) bằng thước và compa:
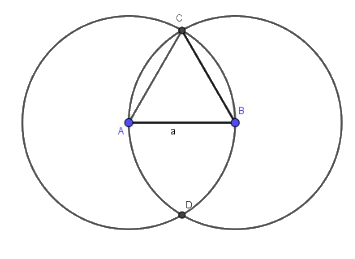
Bước 1. Dùng thước vẽ đoạn thẳng AB = a cm
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC.
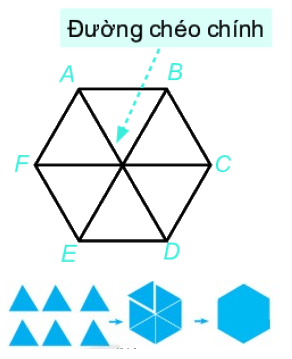
Lục giác đều \(ABCDEF\) có:
- Sáu đỉnh A, B, C, D, E, F
- Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).
- Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau \(AD = BE = CF\).
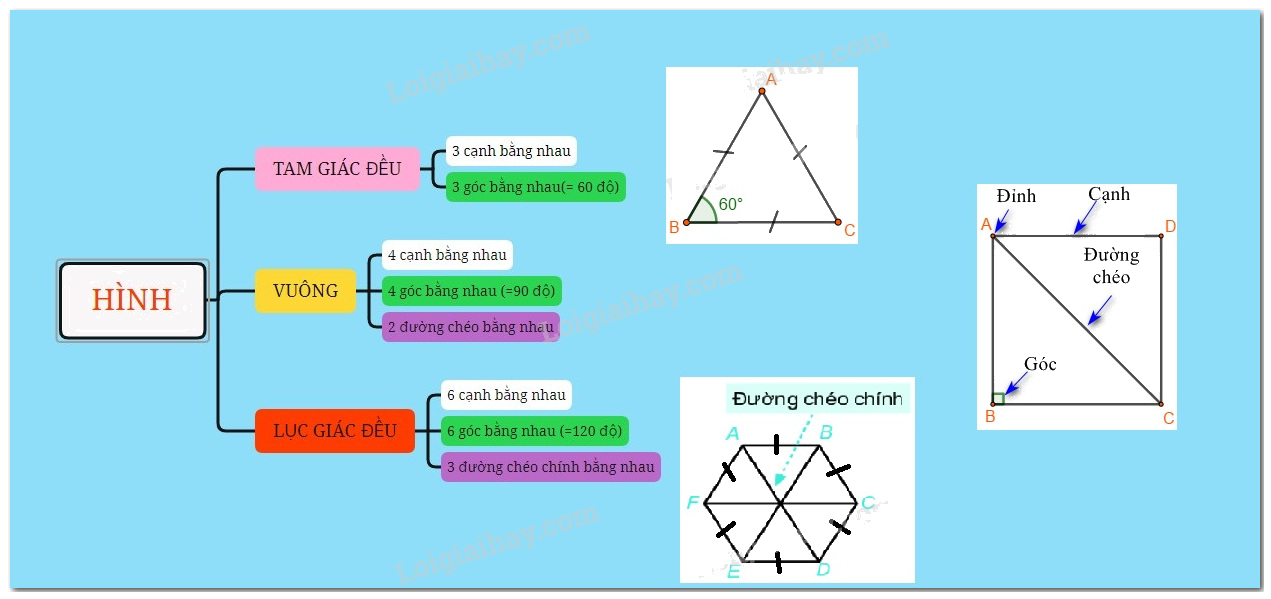
Trong chương trình Toán 6 Chân trời sáng tạo, việc nắm vững kiến thức về các hình đa giác cơ bản như hình vuông, tam giác đều và lục giác đều là vô cùng quan trọng. Những kiến thức này không chỉ là nền tảng cho các bài học tiếp theo mà còn giúp các em phát triển tư duy logic và khả năng giải quyết vấn đề.
Định nghĩa: Hình vuông là hình có bốn cạnh bằng nhau và bốn góc vuông.
Cách vẽ: Có nhiều cách để vẽ hình vuông, ví dụ như sử dụng thước và compa, hoặc sử dụng phần mềm vẽ hình.
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
Cách vẽ: Sử dụng compa để vẽ một đường tròn, sau đó chọn ba điểm trên đường tròn sao cho khoảng cách giữa chúng bằng nhau. Nối ba điểm này lại để được tam giác đều.
Định nghĩa: Lục giác đều là hình có sáu cạnh bằng nhau và sáu góc bằng nhau.
Cách vẽ: Vẽ một đường tròn, sau đó chia đường tròn thành sáu phần bằng nhau. Nối các điểm chia này lại để được lục giác đều.
| Hình | Số cạnh | Số góc | Góc |
|---|---|---|---|
| Hình vuông | 4 | 4 | 90 độ |
| Tam giác đều | 3 | 3 | 60 độ |
| Lục giác đều | 6 | 6 | 120 độ |
Các hình vuông, tam giác đều và lục giác đều xuất hiện rất nhiều trong đời sống hàng ngày. Ví dụ:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về lý thuyết Hình vuông, Tam giác đều và Lục giác đều. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập nhé!