Bài học về Lý thuyết Hình có tâm đối xứng trong chương trình Toán 6 Chân trời sáng tạo là nền tảng quan trọng để các em học sinh hiểu rõ hơn về tính đối xứng trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Lý thuyết Hình có tâm đối xứng Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
1. Hình có tâm đối xứng trong thực tế
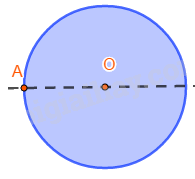
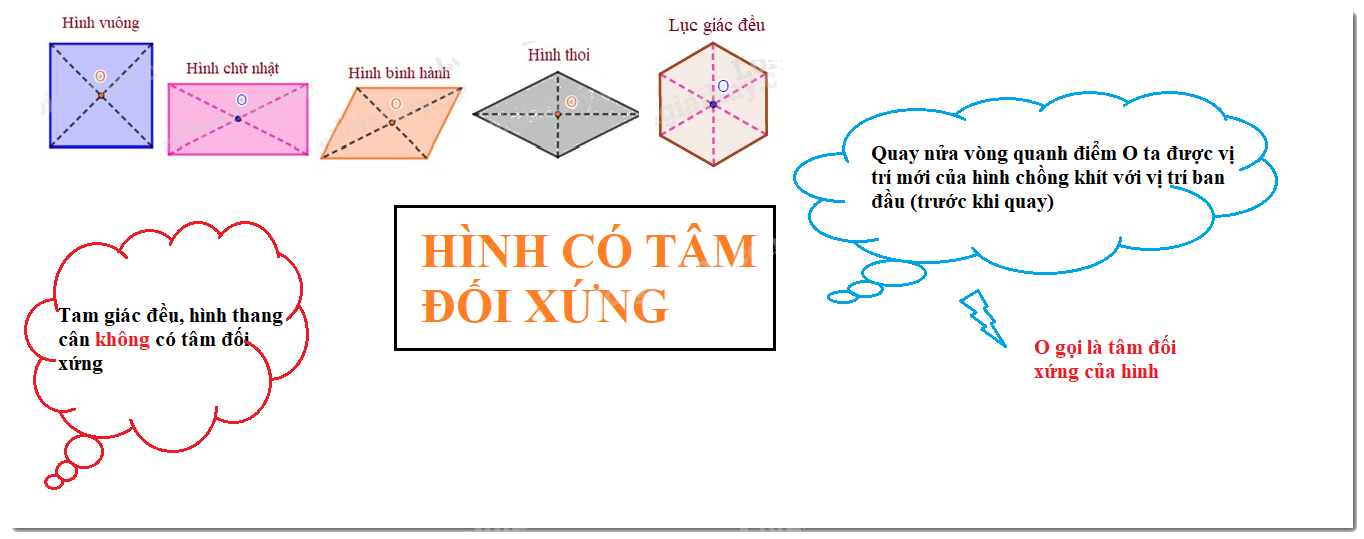
+) Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
+) Hình có tâm đối xứng là các hình: hình tròn, hình chong chóng 2 cánh, chong chóng 4 cánh,...
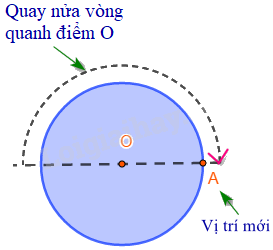
2. Tâm đối xứng của một số hình phẳng
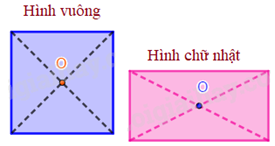
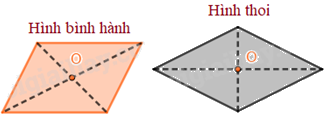
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
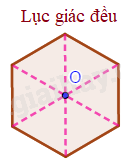
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Lưu ý:
- Có những hình có tâm đối xứng và có nhiều trục đối xứng: Hình tròn, hình vuông, hình chữ nhật, hình thoi.
- Có hình không có tâm đối xứng: Tam giác đều, hình thang cân,..
Trong chương trình Toán 6 Chân trời sáng tạo, khái niệm về hình có tâm đối xứng đóng vai trò quan trọng trong việc phát triển tư duy hình học và khả năng quan sát của học sinh. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, bao gồm định nghĩa, tính chất, cách nhận biết và các ví dụ minh họa.
Một hình được gọi là có tâm đối xứng nếu có một điểm O (gọi là tâm đối xứng) sao cho mọi điểm M của hình đều có một điểm M’ đối xứng với M qua O, và M’ cũng thuộc hình đó. Nói cách khác, nếu ta quay hình 180° quanh tâm đối xứng O, hình mới trùng với hình ban đầu.
Để nhận biết một hình có tâm đối xứng, ta có thể thực hiện các bước sau:
Một số ví dụ về hình có tâm đối xứng:
Hình có tâm đối xứng khác với hình có trục đối xứng. Hình có trục đối xứng là hình có một đường thẳng (trục đối xứng) sao cho nếu gập hình theo đường thẳng đó, hai nửa hình trùng khít lên nhau. Trong khi đó, hình có tâm đối xứng là hình có một điểm (tâm đối xứng) sao cho nếu quay hình 180° quanh điểm đó, hình mới trùng với hình ban đầu.
Hãy xác định xem các hình sau có tâm đối xứng hay không:
Lý thuyết về hình có tâm đối xứng có nhiều ứng dụng trong thực tế, chẳng hạn như trong kiến trúc, nghệ thuật, thiết kế và các lĩnh vực khoa học khác. Việc hiểu rõ về tính đối xứng giúp chúng ta tạo ra những sản phẩm đẹp mắt, hài hòa và cân đối.
Để hiểu sâu hơn về lý thuyết hình học, các em có thể tìm hiểu thêm về các khái niệm liên quan như phép đối xứng tâm, phép quay, và các loại hình đối xứng khác.
Lý thuyết Hình có tâm đối xứng Toán 6 Chân trời sáng tạo là một phần quan trọng của chương trình học. Việc nắm vững kiến thức này sẽ giúp các em học sinh phát triển tư duy hình học, khả năng quan sát và giải quyết các bài toán thực tế một cách hiệu quả. Hãy luyện tập thường xuyên và áp dụng kiến thức vào các bài tập để đạt kết quả tốt nhất.