Chào mừng các em học sinh đến với bài học về lý thuyết so sánh phân số trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất để có thể so sánh các phân số một cách chính xác và hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu các phương pháp so sánh phân số khác nhau, từ việc quy đồng mẫu số đến việc sử dụng tính chất của phân số. Đồng thời, bài học cũng sẽ giúp các em hiểu rõ hơn về ứng dụng của việc so sánh phân số trong thực tế.
Lý thuyết So sánh phân số Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
I. So sánh hai phân số cùng mẫu
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$.
Ta có: $ - 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ:
So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$
Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$
Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$.
Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)
Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$.
$BCNN(12;18) = 36$ nên ta có:
$\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$
$\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$.
Vì $ - 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$.
Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn $0$, gọi là phân số dương.
Ví dụ:$\dfrac{{ - 3}}{{ - 5}} > 0$ hoặc $\dfrac{4}{5} > 0$
Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn $0$, gọi là phân số âm.
Ví dụ : $\dfrac{{ - 3}}{5} < 0$
- Ta còn có các cách so sánh phân số như sau:
+ Áp dụng tính chất: $\dfrac{a}{b} < \dfrac{c}{d} \Leftrightarrow a.d < b.c{\rm{\;}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in {\rm{Z}};{\rm{b}},{\rm{d\;}} > {\rm{\;0}})$
+ Đưa về hai phân số cùng tử dương rồi so sánh mẫu (chỉ áp dụng đối với hai phân số cùng âm hoặc cùng dương)
Ví dụ: $\dfrac{4}{{ - 9}} > \dfrac{4}{{ - 7}};$$\dfrac{3}{5} < \dfrac{3}{2}$
+ Chọn số thứ ba làm trung gian.
Ví dụ:
$\dfrac{{ - 4}}{9} < 0 < \dfrac{4}{7}{\kern 1pt}$ suy ra $\dfrac{{ - 4}}{9}<\dfrac{4}{7}$
$\dfrac{{14}}{9} > 1 > \dfrac{4}{7}$ suy ra $\dfrac{{14}}{9}>\dfrac{4}{7}$
+ Sử dụng tính chất so sánh: Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}\)
IV. Hỗn số dương
Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 ( với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.
Ví dụ:
\(\frac{7}{4}= \frac{4.1+3}{4}= 1 + \frac{3}{4}=1\frac{3}{4}\)
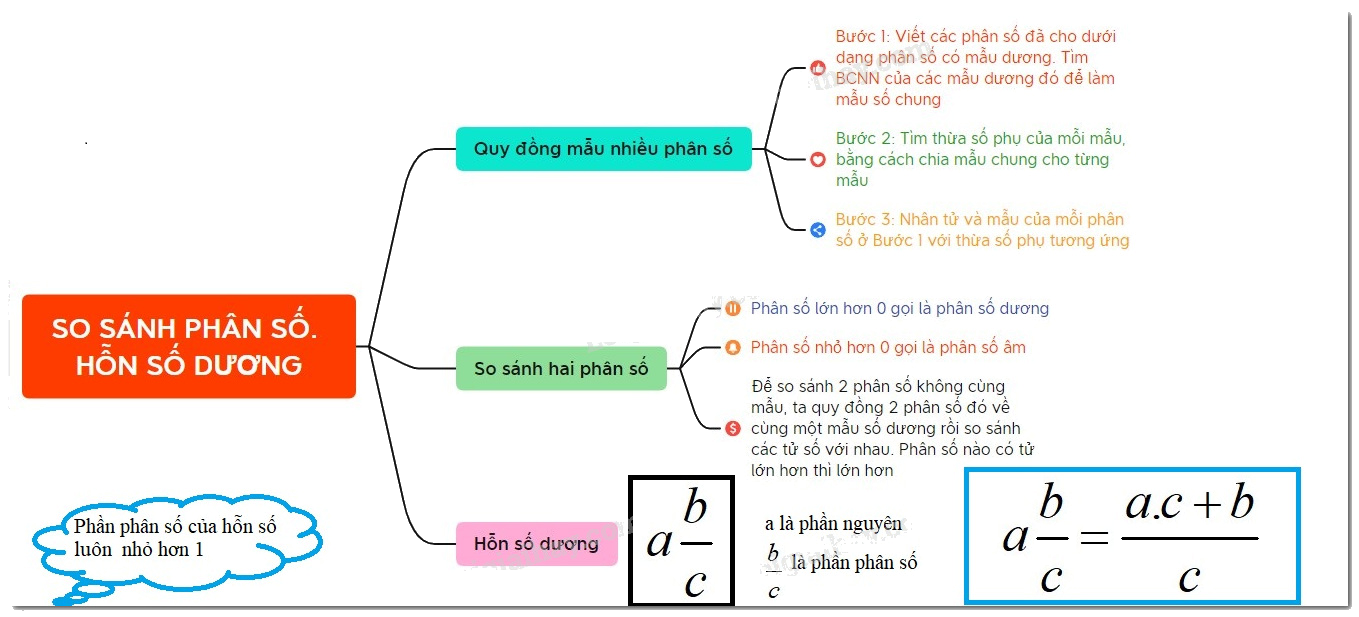
Trong chương trình Toán 6, việc so sánh phân số là một kỹ năng cơ bản và quan trọng. Nó giúp học sinh hiểu rõ hơn về giá trị của phân số và ứng dụng trong các bài toán thực tế. Bài viết này sẽ trình bày chi tiết lý thuyết so sánh phân số theo chương trình Chân trời sáng tạo, cùng với các ví dụ minh họa và bài tập thực hành.
Phân số là biểu thức của một phần của một đơn vị. Một phân số có dạng a/b, trong đó:
Có nhiều phương pháp để so sánh phân số, trong đó phổ biến nhất là:
Ví dụ 1: So sánh hai phân số 2/3 và 3/4.
Ta quy đồng mẫu số của hai phân số: 2/3 = 8/12 và 3/4 = 9/12.
Vì 8/12 < 9/12 nên 2/3 < 3/4.
Ví dụ 2: So sánh hai phân số 5/7 và 5/9.
Vì hai phân số có cùng tử số, ta so sánh các mẫu số. Vì 7 < 9 nên 5/7 > 5/9.
Hãy so sánh các phân số sau:
Việc so sánh phân số là một kỹ năng quan trọng trong Toán học. Bằng cách nắm vững các phương pháp so sánh phân số, các em có thể giải quyết các bài toán một cách nhanh chóng và chính xác. Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích về lý thuyết so sánh phân số Toán 6 Chân trời sáng tạo.