Chào mừng các em học sinh đến với bài học về lý thuyết lũy thừa với số mũ tự nhiên trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về lũy thừa, giúp các em tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất và cách áp dụng lũy thừa vào giải toán một cách hiệu quả. Hãy cùng bắt đầu nhé!
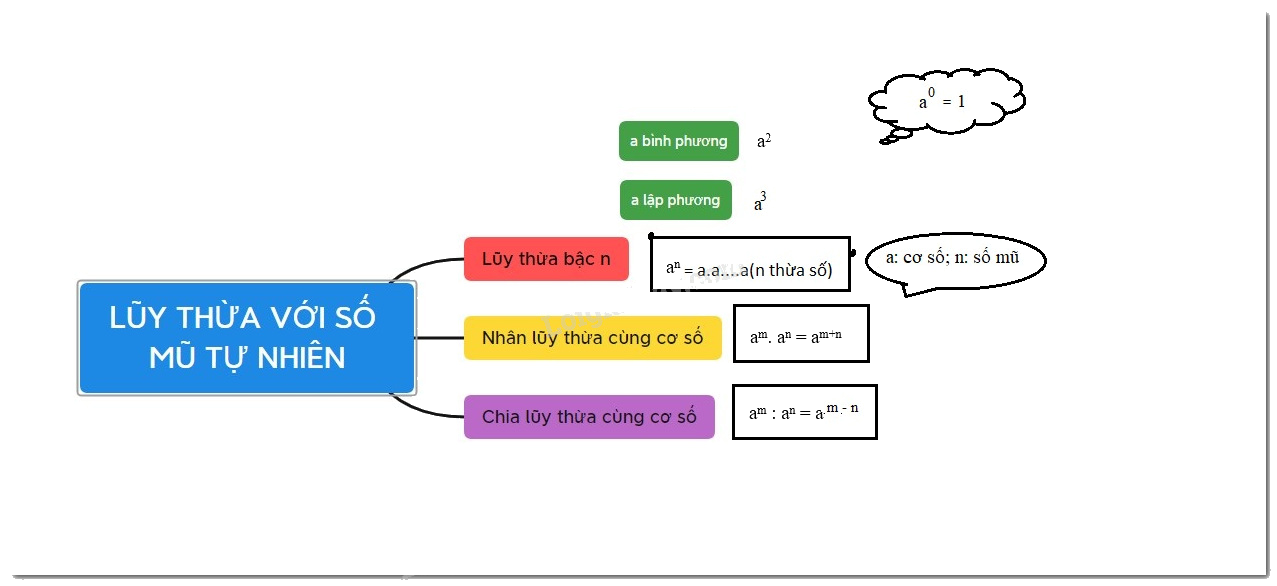
Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
\({a^n} = a.a \ldots ..a\) (\(n\) thừa số \(a\) ) (\(n \notin \mathbb{N}^*\) )
\({a^n}\) đọc là “a mũ n” hoặc “a lũy thừa n”.
\(a\) được gọi là cơ số.
\(n\) được gọi là số mũ.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
\({a^1} = a\)
\({a^2} = a.a\) gọi là “\(a\) bình phương” (hay bình phương của \(a\)).
\({a^3} = a.a.a\) gọi là “\(a\) lập phương” (hay lập phương của \(a\)).
Với \(n\) là số tự nhiên khác 0 (thuộc \(\mathbb{N}^*\)), ta có: \({10^n} = 1\underbrace {0...0}_{n{\rm{ \,chữ\, số\, 0}}}\)(số mũ là n thì có n chữ số 0 đằng sau chữ số 1)
Quy ước: \({a^1} = a\); \({a^0} = 1\left( {a \ne 0} \right).\)
Ví dụ:
a) \({8^3}\) đọc là “tám mũ ba”, có cơ số là 8 và số mũ là 3.
b) Tính \({2^3}\).
Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
\({2^3} = 2.2.2 = 8\)
c) Tính \({10^3}\)
\({10^3}\) có số mũ là 3 nên \({10^3} = 1000\)(Sau chữ số 1 có 3 chữ số 0).
d) Viết 10 000 000 dưới dạng lũy thừa của 10:
Cách 1: \(10000000 = 10.10.10.10.10.10.10\)\( = {10^7}\)
Cách 2: Sau chữ số 1 có 7 chữ số 0 nên \(10000000 = {10^7}\)
e) Viết 16 dưới dạng lũy thừa cơ số 4:
\(16 = 4.4 = {4^2}\)
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
\({a^m}.{a^n} = {a^{m + n}}\)
Ví dụ:
a) \({3.3^5} = {3^1}{.3^5} = {3^{1 + 5}} = {3^6}.\)
b) \({5^2}{.5^4} = {5^{2 + 4}} = {5^6}\)
c) \({a^3}.{a^5} = {a^{3 + 5}} = {a^8}\)
d) \(x.{x^8} = {x^1}.{x^8} = {x^{1 + 8}} = {x^9}\)
e) \({4^2}.64 = {4^2}.4.4.4 = {4^2}{.4^3} = {4^{2 + 3}} = {4^5}\)
f) \(10.2.5 = 10.\left( {2.5} \right) = 10.10 = {10^2}\) (Sử dụng tính chất kết hợp trong phép nhân trước).
Phép chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
\({a^m}:{a^n} = {a^{m - n}}\) \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)
Ví dụ:
a) \({3^5}:3 = {3^5}:{3^1} = {3^{5 - 1}} = {3^4}\)\( = 3.3.3.3 = 81\)
b) \({a^6}:{a^2} = {a^{6 - 2}} = {a^4}\)
c) \({2^3}:{2^3} = {2^{3 - 3}} = {2^0} = 1\)
d) \(81:{3^2} = {3^4}:{3^2} = {3^{4 - 2}} = {3^2} = 3.3 = 9\)
Lưu ý:
Phép chia hai lũy thừa cùng cơ số không thể lấy hai số mũ chia cho nhau mà phải lấy hai số mũ trừ cho nhau.
Lũy thừa là một khái niệm quan trọng trong toán học, đặc biệt là ở chương trình Toán 6. Hiểu rõ lý thuyết lũy thừa sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác. Bài viết này sẽ trình bày chi tiết lý thuyết lũy thừa với số mũ tự nhiên theo chương trình Chân trời sáng tạo.
Lũy thừa của một số tự nhiên a (gọi là cơ số) với số mũ tự nhiên n (n > 0) là tích của n thừa số a, ký hiệu là an. Ví dụ: 23 = 2 x 2 x 2 = 8.
Có một số trường hợp lũy thừa cần được lưu ý:
Các tính chất của lũy thừa giúp đơn giản hóa các phép tính và giải quyết bài toán một cách hiệu quả:
Để so sánh các lũy thừa, ta có thể sử dụng các phương pháp sau:
Bài 1: Tính giá trị của các biểu thức sau:
Bài 2: Viết các biểu thức sau dưới dạng lũy thừa:
Lũy thừa được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học, ví dụ:
Bài học về lý thuyết lũy thừa với số mũ tự nhiên Toán 6 Chân trời sáng tạo đã cung cấp cho các em những kiến thức cơ bản và quan trọng nhất. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan. Chúc các em học tốt!
| Lũy thừa | Giá trị |
|---|---|
| 23 | 8 |
| 52 | 25 |