Phân số là một khái niệm quan trọng trong toán học, đặc biệt là ở chương trình lớp 6. Việc nắm vững lý thuyết Tính chất cơ bản của phân số là nền tảng để giải quyết các bài toán liên quan đến phân số một cách hiệu quả.
Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu về các tính chất cơ bản của phân số, cùng với các ví dụ minh họa cụ thể để bạn có thể áp dụng vào thực tế.
Lý thuyết Tính chất cơ bản của phân số Toán 6 Chân tời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$ .
Ví dụ:
a) $\dfrac{2}{3} = \dfrac{{2.4}}{{3.4}} = \dfrac{8}{{12}}$
b) $\dfrac{{ - 5}}{7} = \dfrac{{ - 5.2}}{{7.2}} = \dfrac{{ - 10}}{{14}}$
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng ta được một phân số mới bằng phân số đã cho.
$\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$ với $n \in $ƯC$\left( {a;b} \right)$.
Ví dụ:
a) $\dfrac{9}{{15}} = \dfrac{{9:3}}{{15:3}} = \dfrac{3}{5}$
b) $\dfrac{{ - 14}}{{ - 21}} = \dfrac{{ - 14:7}}{{ - 21:7}} = \dfrac{2}{3}$
Bước 1: Viết các phân số đã cho về phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.
Ví dụ:
Để quy đồng mẫu hai phân số $\dfrac{1}{6}$ và $\dfrac{3}{{ - 8}}$, ta làm như sau:
- Đưa về phân số có mẫu dương: $\dfrac{1}{6}$ và $\dfrac{{ - 3}}{8}$
- Tìm mẫu chung: $BC(6;\,8) = 24$
- Tìm thừa số phụ: $24:6 = 4;\,24:8 = 3$
- Ta có: $\dfrac{1}{6} = \dfrac{{1.4}}{{6.4}} = \dfrac{4}{{24}}$ và $\dfrac{3}{{ - 8}} = \dfrac{{ - 3}}{8} = \dfrac{{ - 3.3}}{{8.3}} = \dfrac{{ - 9}}{{24}}$.
a) Khái niệm phân số tối giản:
Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là $1$ và $ - 1$
b) Cách rút gọn phân số
Bước 1: Tìm ƯCLN của tử và mẫu khi đã bỏ dấu “-” (nếu có)
Bước 2: Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản.
Ví dụ:
Để rút gọn phân số $\dfrac{{ - 15}}{{24}}$ ta làm như sau:
- Tìm ƯCLN của mẫu: ƯCLN(15; 24)=3.
- Chia cả tử và mẫu cho ƯCLN: $\dfrac{{ - 15}}{{24}} = \dfrac{{ - 15:3}}{{24:3}} = \dfrac{{ - 5}}{8}$.
Ta được $\dfrac{{ - 5}}{8}$ là phân số tối giản.
Áp dụng tính chất cơ bản của phân số
$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$; $\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$với $n \in $ ƯC$\left( {a;b} \right)$.
Áp dụng tính chất cơ bản của phân số để biến đổi hai phân số đã cho thành hai phân số bằng chúng nhưng có từ (hoặc mẫu) như nhau. Khi đó mẫu (hoặc tử) của chúng phải bằng nhau. Từ đó tìm được số chưa biết.Hoặc áp dụng định nghĩa hai phân số bằng nhau.
- Chia cả tử và mẫu của phân số $\dfrac{a}{b}$ cho ƯCLN của $a$ và $b$ để rút gọn thành phân số tối giản ( bỏ dấu “-” nếu có)
- Trường hợp biểu thức có dạng phân số, ta cần làm xuất hiện các thừa số chung của tử và mẫu rồi rút gọn các thừa số chung đó.
Để tìm phân số tối giản trong các phân số cho trước, ta tìm ƯCLN của tử và mẫu đối với từng phân số. Phân số nào có ƯCLN này là $1$ thì đó là phân số tối giản.
Ví dụ:
Phân số $\dfrac{{ - 5}}{7}$ tối giản vì ƯCLN $\left( {5,7} \right) = 1.$
Ta thực hiện hai bước:
- Rút gọn phân số đã cho đến tối giản, chằng hạn ta được phân số tối giản $\dfrac{m}{n}$ ;
- Dạng tổng quát của các phân số phải tìm là $\dfrac{{m.k}}{{n.k}}$ ($k$$ \in $$\mathbb{Z}$, $k$$ \ne 0).$
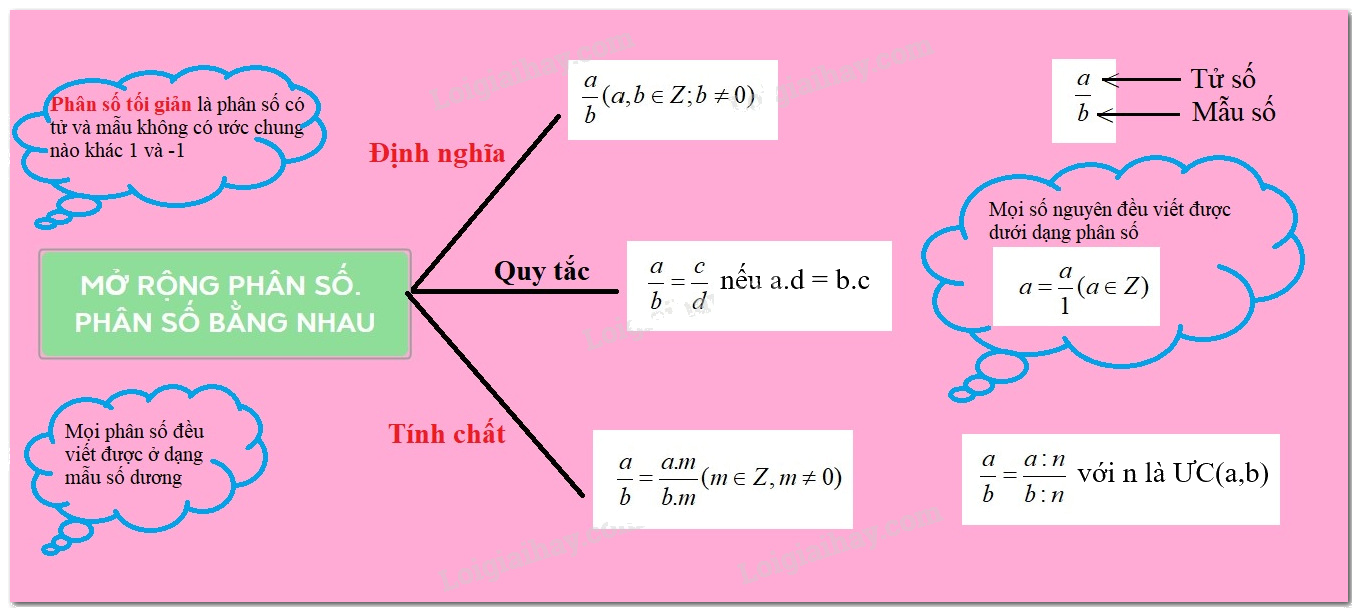
Phân số là một biểu thức toán học thể hiện một phần của một tổng thể. Nó được biểu diễn dưới dạng a/b, trong đó a là tử số và b là mẫu số. Mẫu số (b) luôn khác 0.
Hai phân số được gọi là bằng nhau nếu chúng biểu diễn cùng một lượng. Ví dụ, 1/2 và 2/4 là hai phân số bằng nhau vì chúng đều biểu diễn một nửa.
Tính chất: Nếu a/b = c/d thì ad = bc.
Ví dụ: Kiểm tra xem 3/5 và 9/15 có bằng nhau không. Ta có 3 * 15 = 45 và 5 * 9 = 45. Vì vậy, 3/5 = 9/15.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho ước chung lớn nhất (ƯCLN) của chúng. Việc rút gọn phân số giúp phân số trở nên đơn giản hơn, dễ hiểu hơn.
Ví dụ: Rút gọn phân số 12/18.
Quy đồng mẫu số là việc biến đổi các phân số có mẫu số khác nhau thành các phân số có cùng mẫu số. Việc quy đồng mẫu số giúp việc so sánh và thực hiện các phép toán trên phân số trở nên dễ dàng hơn.
Cách quy đồng mẫu số:
Ví dụ: Quy đồng mẫu số của 1/2 và 1/3.
Nếu a/b = c/d thì:
Các tính chất cơ bản của phân số được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến phân số, bao gồm:
Bài 1: Rút gọn các phân số sau: 15/25, 18/24, 21/35
Bài 2: Quy đồng mẫu số của các phân số sau: 2/3 và 3/4, 1/5 và 2/7
Bài 3: Kiểm tra xem các phân số sau có bằng nhau không: 4/6 và 8/12, 5/7 và 10/14
Việc hiểu rõ lý thuyết Tính chất cơ bản của phân số là vô cùng quan trọng để học tốt môn Toán. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập một cách hiệu quả. Chúc bạn học tốt!