Chào mừng các em học sinh đến với bài học về Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về đoạn thẳng, giúp các em hiểu rõ hơn về khái niệm, tính chất và cách tính độ dài của đoạn thẳng.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng, dễ hiểu và phù hợp với từng đối tượng học sinh.
Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Bài 4. Đoạn thẳng. Độ dài đoạn thẳng
1. Đoạn thẳng
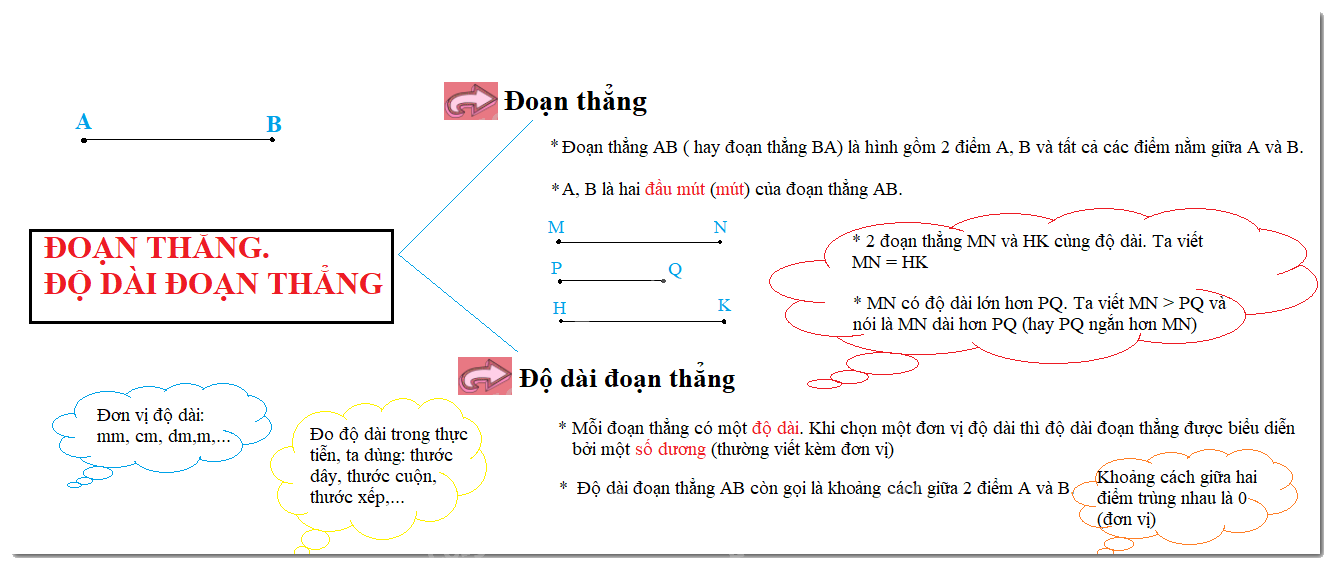
Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa giữa A và B.
Đoạn thẳng AB còn gọi là đoạn thẳng BA.
Hai điểm A, B gọi là hai đầu mút (hoặc hai đầu) của đoạn thẳng AB.
2. Độ dài đoạn thẳng
Nhận xét:
- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.
- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B.
- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.
3. So sánh hai đoạn thẳng
Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.
4. Một số dụng cụ đo độ dài
Một số dụng cụ đo độ dài, đo khoảng cách trong thực tiễn: thước cuộn, thước xếp, thước dây.
Trong hình học, đoạn thẳng là một khái niệm cơ bản và quan trọng. Nó là một phần của đường thẳng được giới hạn bởi hai điểm, gọi là mút đoạn thẳng. Hiểu rõ về đoạn thẳng là nền tảng để học các khái niệm hình học phức tạp hơn.
Đoạn thẳng AB là hình gồm tất cả các điểm nằm trên đường thẳng AB và nằm giữa hai điểm A và B. Ký hiệu đoạn thẳng AB là AB (hoặc BA).
Độ dài đoạn thẳng là khoảng cách giữa hai mút của đoạn thẳng. Độ dài đoạn thẳng AB được ký hiệu là AB. Đơn vị đo độ dài đoạn thẳng thường là mét (m), centimet (cm), milimet (mm),...
Để đo độ dài đoạn thẳng, ta sử dụng thước đo. Đặt thước đo sao cho một đầu của thước trùng với một mút của đoạn thẳng, sau đó đọc số đo ở mút còn lại. Lưu ý, cần chọn thước đo có độ chia phù hợp với độ dài của đoạn thẳng.
Có ba trường hợp xảy ra khi so sánh độ dài hai đoạn thẳng:
Trung điểm của đoạn thẳng AB là điểm M nằm trên đoạn thẳng AB sao cho AM = MB. Điểm M được gọi là trung điểm của đoạn thẳng AB.
Nếu M là trung điểm của đoạn thẳng AB, thì:
AB = 2 * AM = 2 * MB
Ví dụ 1: Cho đoạn thẳng AB có độ dài 8cm. Gọi M là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng AM và MB.
Giải: Vì M là trung điểm của đoạn thẳng AB, nên AM = MB = AB / 2 = 8cm / 2 = 4cm.
Ví dụ 2: Cho đoạn thẳng CD có độ dài 12cm. Gọi N là một điểm nằm trên đoạn thẳng CD sao cho CN = 3cm. Tính độ dài đoạn thẳng ND.
Giải: Vì N nằm trên đoạn thẳng CD, nên CD = CN + ND. Suy ra ND = CD - CN = 12cm - 3cm = 9cm.
Lý thuyết đoạn thẳng có ứng dụng rộng rãi trong thực tế, ví dụ như:
Để nắm vững kiến thức về lý thuyết đoạn thẳng, các em nên luyện tập thường xuyên các bài tập trong sách giáo khoa và các tài liệu tham khảo. Hãy tìm hiểu thêm về các khái niệm liên quan như đường thẳng, tia, góc để có cái nhìn toàn diện hơn về hình học.
Bài học về Lý thuyết Đoạn thẳng. Độ dài đoạn thẳng Toán 6 Chân trời sáng tạo đã cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về đoạn thẳng. Hy vọng rằng, sau bài học này, các em sẽ hiểu rõ hơn về đoạn thẳng và có thể áp dụng kiến thức này vào giải các bài toán thực tế.