Chào mừng các em học sinh đến với bài học về Lý thuyết Trung điểm của đoạn thẳng trong chương trình Toán 6 Chân trời sáng tạo. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về trung điểm, giúp các em giải quyết các bài tập liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa trung điểm, cách xác định trung điểm của một đoạn thẳng, và các ứng dụng thực tế của lý thuyết này trong cuộc sống.
Lý thuyết Trung điểm của đoạn thẳng Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
1. Trung điểm của đoạn thẳng
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.
Tóm tắt:
\(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow $${\rm{IA = IB}}$ và \(I\) nằm giữa hai điểm \(A;B.\)
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AI + IB = AB\\{\rm{IA = IB}}\end{array} \right.$
hoặc \(I\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AI = BI = }}\dfrac{1}{2}AB$
2. Cách vẽ trung điểm của đoạn thẳng
Giả sử ta cần vẽ trung điểm M của đoạn thẳng AB có độ dài 5 cm.
Cách 1:
- Đặt mép thước trung với đoạn thẳng AB sao cho vạch 0 trùng với điểm A, khi đó điểm B trùng với vạch chỉ số 5 trên thước.
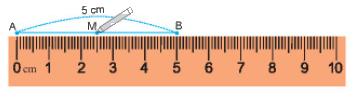
- Ta lấy điểm M trùng với vạch chỉ số 2,5 cm trên thước, Khi đó ta có M là trung điểm của đoạn thẳng AB.
Cách 2:
Vẽ đoạn thẳng AB trên giấy can. Gấp giấy sao cho điểm B trùng với điểm A. Giao của nếp gấp và đoạn thẳng AB chính là trung điểm M cần xác định

Trong chương trình Toán 6 Chân trời sáng tạo, kiến thức về trung điểm của đoạn thẳng là một nền tảng quan trọng để xây dựng các khái niệm hình học phức tạp hơn. Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết này, bao gồm định nghĩa, tính chất, và các ứng dụng thực tế.
Trung điểm M của đoạn thẳng AB là điểm sao cho MA = MB. Nói cách khác, M nằm giữa A và B và cách đều hai điểm A và B.
Có nhiều cách để xác định trung điểm của một đoạn thẳng:
xM = (xA + xB) / 2
yM = (yA + yB) / 2
Trung điểm của một đoạn thẳng có những tính chất quan trọng sau:
Lý thuyết trung điểm có nhiều ứng dụng trong thực tế và trong các bài toán hình học:
Ví dụ 1: Cho đoạn thẳng AB có độ dài 10cm. Tìm trung điểm M của đoạn thẳng AB.
Giải: Vì M là trung điểm của đoạn thẳng AB nên MA = MB = AB / 2 = 10cm / 2 = 5cm.
Ví dụ 2: Cho hai điểm A(1, 2) và B(5, 6). Tìm tọa độ trung điểm M của đoạn thẳng AB.
Giải: Sử dụng công thức tính tọa độ trung điểm, ta có:
xM = (1 + 5) / 2 = 3
yM = (2 + 6) / 2 = 4
Vậy tọa độ trung điểm M là (3, 4).
Lý thuyết Trung điểm của đoạn thẳng là một kiến thức cơ bản nhưng vô cùng quan trọng trong chương trình Toán 6 Chân trời sáng tạo. Việc nắm vững lý thuyết này sẽ giúp các em giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và áp dụng vào thực tế.