Bài 10.12 trang 65 sách bài tập Toán 7 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
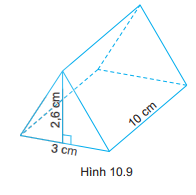
Một lăng kính thuỷ tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước như trong Hình 10.9 a)Tính thể tích của lăng kính thuỷ tinh. b)Người ta làm một chiếc hộp bằng bìa cứng để đựng vừa khít lăng kính thuỷ tinh nói trên (hở hai đáy tam giác). Tính diện tích bìa cần dùng (bỏ qua mép nối).
Đề bài
Một lăng kính thuỷ tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước như trong Hình 10.9
a)Tính thể tích của lăng kính thuỷ tinh.
b)Người ta làm một chiếc hộp bằng bìa cứng để đựng vừa khít lăng kính thuỷ tinh nói trên (hở hai đáy tam giác). Tính diện tích bìa cần dùng (bỏ qua mép nối).
Phương pháp giải - Xem chi tiết
a)Thể tích: \(V = {S_{day}}.h\)
b)Diện tích bìa cần dùng chính là diện tích xung quanh hình lăng trụ đứng.
Lời giải chi tiết
a)
Diện tích đáy của lăng kính là: \(S = \dfrac{1}{2}.3.2,6 = 3,9\left( {c{m^2}} \right)\)
Thể tích lăng kính thuỷ tinh là: \(V = S.h = 3,9.10 = 39\left( {c{m^3}} \right)\)
b)
Chu vi đáy là: C = 3 + 3 + 3 = 9 (cm)
Diện tích bìa cứng cần dùng là:
\({S_{xp}} = {C_{day}}.h = 9.10 = 90\left( {c{m^2}} \right)\)
Bài tập 10.12 trang 65 sách bài tập Toán 7 Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc khi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các định nghĩa và tính chất sau:
Đề bài: (Sách bài tập Toán 7 tập 1 - Kết nối tri thức với cuộc sống)
Cho hình vẽ sau:
(Hình vẽ minh họa hai đường thẳng a và b song song, bị cắt bởi đường thẳng c, tạo thành các góc được đánh số)
a) Tính số đo các góc còn lại trong hình.
b) Chứng minh rằng AB song song với CD.
a) Giả sử góc A1 = 60 độ. Vì a // b nên:
b) Để chứng minh AB // CD, ta cần chứng minh một trong các điều kiện sau:
Trong trường hợp này, ta có thể chứng minh bằng cách sử dụng hai góc so le trong. Giả sử góc ACD = 60 độ. Vì góc ACD và góc CAB là hai góc so le trong và bằng nhau (đều bằng 60 độ) nên AB // CD (theo dấu hiệu nhận biết hai đường thẳng song song).
Để hiểu rõ hơn về các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em có thể thực hiện các bài tập sau:
Bài tập 10.12 trang 65 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.