Bài 9.20 trang 58 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các góc so le trong, đồng vị, trong cùng phía và góc kề bù.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.20, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S.Chứng minh tia PO là tia phân giác của góc RPS.
Đề bài
Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S.Chứng minh tia PO là tia phân giác của góc RPS.
Phương pháp giải - Xem chi tiết
-O, R cùng nằm trên đường trung trực PM, chứng minh \(\widehat {OPR} = \widehat {OMR}\).
-O,S cùng nằm trên đường trung trực PN, chứng minh \(\widehat {OPS} = \widehat {ONS}\).
Lời giải chi tiết
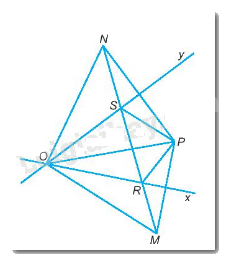
Ta có: O, R nằm trên đường trung trực của PM
\( \Rightarrow OP = OM;RP = RM\) (1)
\( \Rightarrow \)Tam giác OPM cân tại O, tam giác RPM cân tại R.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPM} = \widehat {OMP}\\\widehat {RPM} = \widehat {RMP}\end{array} \right.\\ \Rightarrow \widehat {OPR} = \widehat {OMR}\end{array}\)
Tương tự: O, S nằm trên đường trung trực của PN
\( \Rightarrow OP = ON;SP = SN\)(2)
\( \Rightarrow \)Tam giác OPN cân tại O, tam giác SPN cân tại S.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPN} = \widehat {ONP}\\\widehat {SPN} = \widehat {SNP}\end{array} \right.\\ \Rightarrow \widehat {OPS} = \widehat {ONS}\end{array}\)
Từ (1) và (2) suy ra: OM = ON = OP hay OM = ON
\( \Rightarrow \)Tam giác OMN cân tại O
\( \Rightarrow \widehat {OMN} = \widehat {ONM}\)
Hay \(\widehat {OMR} = \widehat {ONS}\)
\( \Rightarrow \widehat {OPR} = \widehat {OPS}\) Vậy tia PO là tia phân giác của góc RPS.
Bài 9.20 sách bài tập Toán 7 Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để chứng minh một số tính chất hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và định lý sau:
Đề bài: Cho hình vẽ, biết a // b và góc A1 = 40°. Tính các góc còn lại trên hình.
Lời giải:
Kết luận: Các góc còn lại trên hình có số đo lần lượt là: A2 = 140°, B1 = 40°, B2 = 140°, A3 = 140°, B3 = 140°, B4 = 40°.
Để hiểu sâu hơn về các góc tạo bởi đường thẳng cắt đường thẳng, các em có thể tham khảo thêm các bài tập tương tự sau:
Các bài tập này sẽ giúp các em rèn luyện kỹ năng vận dụng các định lý và tính chất liên quan đến các góc tạo bởi đường thẳng cắt đường thẳng, từ đó nâng cao khả năng giải toán hình học.
Khi giải các bài tập về góc tạo bởi đường thẳng cắt đường thẳng, các em cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh sẽ tự tin giải bài 9.20 trang 58 sách bài tập Toán 7 Kết nối tri thức với cuộc sống một cách hiệu quả. Chúc các em học tốt!