Bài 12 trang 70 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số hữu tỉ. Bài tập này đòi hỏi học sinh phải nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ và áp dụng chúng một cách linh hoạt.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 12 trang 70 sách bài tập Toán 7 Kết nối tri thức với cuộc sống, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
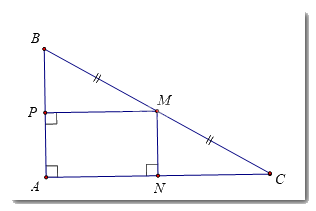
Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:
a)\(\Delta MNC = \Delta BPM\)
b)\(\widehat {NMP} = {90^0}\)
Phương pháp giải - Xem chi tiết
a) \( \Delta MNC = \Delta BPM\left( {ch - gn} \right)\)
b) Chứng minh tứ giác MNAP là hình chữ nhật\(\widehat {MCN} = \widehat {BMP}\).
Lời giải chi tiết
a)
Xét \(\Delta MNC\) và \(\Delta BPM\)có:
\(\begin{array}{l}\widehat {MNC} = \widehat {BPM} = {90^0}\\MC = BM\left( {gt} \right)\end{array}\)
\(\widehat {MCN} = \widehat {BMP}\)(cùng phụ với góc B)
\( \Rightarrow \Delta MNC = \Delta BPM\left( {ch - gn} \right)\)
b)
Xét tứ giác MNAP có:
\(\widehat A = \widehat {MPA} = \widehat {MNA} = {90^0}\)
\( \Rightarrow \)Tứ giác MNAP là hình chữ nhật
\( \Rightarrow \widehat {NMP} = {90^0}\)
Bài 12 trang 70 sách bài tập Toán 7 Kết nối tri thức với cuộc sống yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, bao gồm cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc sau:
Dưới đây là lời giải chi tiết cho từng phần của Bài 12 trang 70 sách bài tập Toán 7 Kết nối tri thức với cuộc sống:
Ví dụ: Tính (1/2) + (2/3). Để giải bài này, ta quy đồng mẫu số của hai phân số: (1/2) = (3/6) và (2/3) = (4/6). Sau đó, ta cộng hai phân số: (3/6) + (4/6) = (7/6).
Tương tự, ta thực hiện các phép tính cộng, trừ, nhân, chia khác với số hữu tỉ. Lưu ý, khi thực hiện các phép tính, ta cần rút gọn phân số về dạng tối giản.
Ví dụ: Tìm x biết x + (1/3) = (5/6). Để tìm x, ta trừ cả hai vế của phương trình cho (1/3): x = (5/6) - (1/3). Quy đồng mẫu số: x = (5/6) - (2/6) = (3/6) = (1/2). Vậy x = (1/2).
Khi giải các phương trình tìm x, ta cần áp dụng các quy tắc biến đổi phương trình để đưa phương trình về dạng đơn giản và tìm ra giá trị của x.
Bài toán thực tế thường yêu cầu học sinh áp dụng các kiến thức về số hữu tỉ để giải quyết các vấn đề trong cuộc sống. Ví dụ, bài toán có thể liên quan đến việc tính toán diện tích, chu vi, thời gian, hoặc các đại lượng khác.
Để giải bài toán thực tế, ta cần đọc kỹ đề bài, xác định các đại lượng liên quan, và lập phương trình hoặc sử dụng các phép tính phù hợp để tìm ra đáp án.
Bài 12 trang 70 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ. Hy vọng với lời giải chi tiết và các mẹo học tập trên, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.