Bài 9.16 trang 55 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính toán và chứng minh các mối quan hệ giữa các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 9.16 trang 55 SBT Toán 7 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
a)Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh: JK = BJ + CK. b)Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.
Đề bài
a)Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh: JK = BJ + CK.
b)Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.
Phương pháp giải - Xem chi tiết
a)Chứng minh tam giác JIB cân tại J, tam giác IKC cân tại K
b)Áp dụng: 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
BI vuông góc BI’ suy ra BI’ là phân giác góc ngoài tại B
Lời giải chi tiết
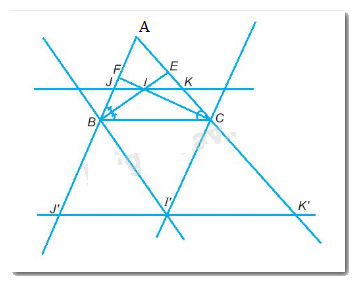
a)
Ta có: BI là phân giác góc FBC
\( \Rightarrow \widehat {JBI} = \widehat {IBC}\)
Lại có: JK // BC
\( \Rightarrow \widehat {JIB} = \widehat {IBC}\)(2 góc so le trong)
\( \Rightarrow \widehat {JBI} = \widehat {JIB}\)\(\)
\( \Rightarrow \Delta JIB\)cân tại J
\( \Rightarrow JI = JB\)
Chứng minh tương tự: KI = KC
Ta có:
\(JK = JI + IK = JB + CK\)
b)
Ta có: \(BI' \bot BI\)
\( \Rightarrow BI'\) là tia phân giác của góc tạo bởi BC và tia đối của tia BA (phân giác góc ngoài tại B)
\( \Rightarrow \widehat {J'BI'} = \widehat {I'BC}\) (Tính chất tia phân giác)
Lại có: BC // J’K’
\( \Rightarrow \widehat {CBI'} = \widehat {BI'J'}\) (2 góc so le trong)
\( \Rightarrow \widehat {J'BI'} = \widehat {BI'J'}\)
\( \Rightarrow \Delta J'BI'\) cân tại J’
\( \Rightarrow J'B = J'I'\)
Chứng minh tương tự: K’C = K’I’
Ta có:
J’K’ = J’I’ + I’K’ = BJ’ + CK’ (đpcm)
Bài 9.16 trang 55 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này, học sinh cần nắm vững các kiến thức về góc so le trong, góc đồng vị, góc trong cùng phía và góc ngoài tại đỉnh của một đa giác.
Bài toán thường mô tả một tình huống cụ thể, ví dụ như một con đường cắt ngang một con phố, hoặc hai thanh gỗ được ghép lại với nhau tạo thành một góc. Học sinh cần xác định các góc cần tính, sử dụng các tính chất của các góc đã học để tìm ra mối liên hệ giữa chúng, và từ đó tính ra giá trị của góc cần tìm.
Để giải bài 9.16 trang 55 sách bài tập Toán 7 Kết nối tri thức, học sinh có thể áp dụng các phương pháp sau:
Giả sử bài toán yêu cầu tính góc x trong hình vẽ, biết góc y = 60 độ. Trong trường hợp này, ta có thể sử dụng tính chất hai góc đối đỉnh bằng nhau để suy ra góc x = góc y = 60 độ.
Để rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng, học sinh có thể làm thêm các bài tập tương tự trong sách bài tập Toán 7 Kết nối tri thức, hoặc tìm kiếm trên các trang web học toán online.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng và hình vẽ minh họa nếu cần thiết. Ví dụ:)
Bài 9.16: Cho hình vẽ, biết góc AOB = 40 độ. Tính góc AOC.
Lời giải:
Vì góc AOC và góc AOB là hai góc kề bù nên AOC + AOB = 180 độ.
Suy ra AOC = 180 độ - AOB = 180 độ - 40 độ = 140 độ.
Vậy góc AOC = 140 độ.
Bài 9.16 trang 55 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Bằng cách áp dụng các phương pháp giải phù hợp và rèn luyện thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và đạt kết quả tốt trong học tập.