Chào mừng các em học sinh đến với lời giải chi tiết Bài 15 trang 71 sách bài tập Toán 7 Kết Nối Tri Thức. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải của bài tập này ngay bây giờ!
a)Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A. b)Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước và compa)
Đề bài
a)Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A.
b)Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước và compa)
Phương pháp giải - Xem chi tiết
- MA = MB = MC
- Chỉ ra các tam giác cân và các góc bằng nhau
- Chứng minh góc A bằng 90 độ.
Lời giải chi tiết
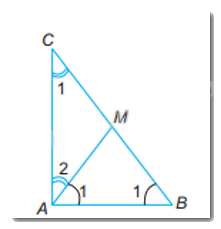
a) Ta có:MA = MB = MC (gt)
\( \Rightarrow \Delta MAB;\Delta MAC\) là hai tam giác cân tại đỉnh M
\( \Rightarrow \left\{ \begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}}\\\widehat {{A_2}} = \widehat {{C_1}}\end{array} \right.\)
Xét tam giác ABC:
\(\widehat A + \widehat B + \widehat C = {180^0}\) (Tổng 3 góc trong 1 tam giác)
\(\begin{array}{l} \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} + \widehat B + \widehat C = {180^0}\\ \Rightarrow \left( {\widehat {{A_1}} + \widehat B} \right) + \left( {\widehat {{A_2}} + \widehat C} \right) = {180^0}\\ \Rightarrow 2\widehat {{A_1}} + 2\widehat {{A_2}} = {180^0}\\ \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = {90^0}\end{array}\)
b)
Vẽ tam giác cân MAB rồi kéo dài BM về phía M đến điểm C sao cho MC = BM. Khi đó tam giác ABC vuông tại A.
Bài 15 trang 71 sách bài tập Toán 7 Kết Nối Tri Thức tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, đặc biệt là các phép toán cộng, trừ, nhân, chia đa thức. Bài tập yêu cầu học sinh phải hiểu rõ các quy tắc về thứ tự thực hiện các phép toán, cũng như các tính chất phân phối của phép nhân đối với phép cộng và phép trừ.
Bài 15 bao gồm một số câu hỏi và bài tập khác nhau, được chia thành các phần nhỏ để học sinh dễ dàng tiếp cận và giải quyết. Các dạng bài tập thường gặp bao gồm:
Để giải câu a), ta cần thực hiện các bước sau:
Ví dụ: Nếu x = 2 và y = -1, thì biểu thức trở thành:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Để rút gọn biểu thức ở câu b), ta cần sử dụng tính chất phân phối của phép nhân đối với phép cộng và phép trừ. Ví dụ:
2(x + y) = 2x + 2y
Để tìm x trong câu c), ta cần giải phương trình. Ví dụ:
x + 3 = 5
x = 5 - 3
x = 2
Khi giải các bài tập về biểu thức đại số, học sinh cần lưu ý những điều sau:
Ví dụ 1: Tính giá trị của biểu thức 5x - 3y khi x = -2 và y = 1.
Giải: 5x - 3y = 5 * (-2) - 3 * 1 = -10 - 3 = -13
Ví dụ 2: Rút gọn biểu thức 4(x - y) + 2x.
Giải: 4(x - y) + 2x = 4x - 4y + 2x = 6x - 4y
Bài 15 trang 71 sách bài tập Toán 7 Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Phép Toán | Quy Tắc |
|---|---|
| Cộng | a + b = b + a |
| Trừ | a - b ≠ b - a |
| Nhân | a * b = b * a |
| Chia | a / b ≠ b / a |