Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm Toán 7 Kết nối tri thức với cuộc sống. Chúng tôi giúp bạn hiểu rõ kiến thức và tự tin làm bài tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những giải pháp học tập hiệu quả nhất.
1. Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
D. Cả ba khẳng định trên đều đúng.
Phương pháp giải:
Tính chất 2 góc đối đỉnh
Lời giải chi tiết:
A. Sai vì 2 góc bằng nhau chưa chắc đã đối đỉnh
B. Sai vì 2 góc không đối đỉnh cũng có thể bằng nhau (chỉ cần số đo của chúng bằng nhau)
C. Đúng
Chọn C
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
A.\({70^0};{70^0};{70^0};{110^0}\) | B. \({60^0};{120^0};{120^0};{120^0};\) |
C. \({80^0};{50^0};{130^0};{100^0};\) | D. \({90^0};{90^0};{90^0};{90^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
Mà 2 góc đối đỉnh thì bằng nhau
Chọn D
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
A. \(\widehat {BOM}\) và \(\widehat {CON}\) | B.\(\widehat {AOB}\) và \(\widehat {AON}\) |
C. \(\widehat {AOM}\) và \(\widehat {CON}\) | D. \(\widehat {COM}\) và \(\widehat {CON}\). |
Phương pháp giải:
+ Vẽ hình
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Lời giải chi tiết:
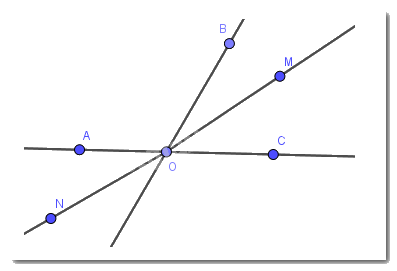
Cặp góc đối đỉnh là cặp góc \(\widehat {AOM}\) và \(\widehat {CON}\)
Chọn C
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = {30^0}\). Số đo của góc AOC bằng:
A.\({30^0};\) | B. \({60^0};\) |
C. \({120^0};\) | D. Một kết quả khác. |
Phương pháp giải:
Nếu OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\)
Hai góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
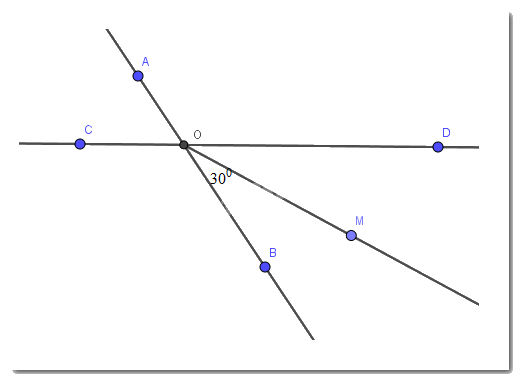
Vì OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\) nên \(\widehat{BOD}=2. \widehat{BOM}=2.30^0=60^0\)
Ta có: \(\widehat{AOC}=\widehat{BOD}\) ( 2 góc đối đỉnh)
Do đó, \(\widehat{AOC}=60^0\)
Chọn B
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là \({65^0}\). Khi đó số đo của ba góc còn lại là:
A.\({65^0};{110^0};{120^0};\) | B. \({65^0};{65^0};{115^0};\) |
C. \({115^0};{115^0};{50^0};\) | D. \({65^0};{115^0};{115^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
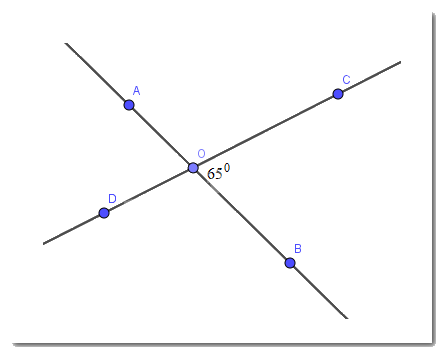
Giả sử hai đường thẳng AB và CD cắt nhau tại O, tạo ra góc BOC có số đo \(65^0\)
\(\Rightarrow \widehat{AOD}=\widehat{BOC}=65^0\) (2 góc đối đỉnh)
\(\widehat{AOB}+\widehat{BOC}=180^0\) (2 góc kề bù) nên \(\widehat{AOB}=180^0-65^0=115^0\)
\(\widehat{COD}=\widehat{AOB}=115^0\) (2 góc đối đỉnh)
Chọn D
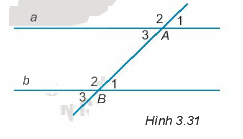
Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu
A.\(\widehat {{A_1}} = \widehat {{B_2}}\)
B. \(\widehat {{A_2}} = \widehat {{B_3}}\)
C. \(\widehat {{A_3}} = \widehat {{B_2}}\)
D. \(\widehat {{A_3}} = \widehat {{B_1}}\)
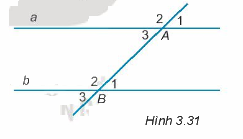
Phương pháp giải:
Dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết:
a//b nếu đường thẳng c cắt hai đường thẳng a và b, tạo thành 1 cặp góc so le trong bằng nhau hoặc 1 cặp góc đồng vị bằng nhau.
Xét khẳng định D:
\(\widehat {{A_3}} = \widehat {{B_1}}\)
Mà 2 góc này ở vị trí so le trong
Do đó, a//b
Chọn D
Cho hình 3.30. Cặp góc \(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc:
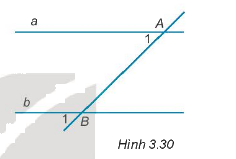
A. So le trong;
B. Đối đỉnh;
C. Đồng vị;
D. Cả ba phương án trên đều sai.
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt
Lời giải chi tiết:
\(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc đồng vị
Chọn C
Cho hình 3.29.
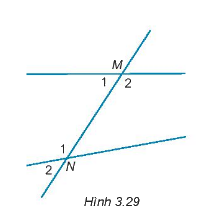
a) Cặp góc so le trong là cặp góc
A.\(\widehat {{M_1}},\widehat {{M_2}};\) | B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
C. \(\widehat {{M_1}},\widehat {{N_2}};\) | D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
b) Cặp góc đồng vị là cặp góc:
A.\(\widehat {{M_1}},\widehat {{M_2}};\) | B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
C. \(\widehat {{M_1}},\widehat {{N_2}};\) | D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt.
Lời giải chi tiết:
a) Chọn D
b) Chọn C
Cho Hình 3.32, biết \(a// b\).
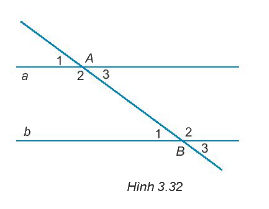
Khẳng định nào sau đây là sai?
A.\(\widehat {{A_1}} > \widehat {{B_1}}\)
B. \(\widehat {{A_2}} = \widehat {{B_2}}\)
C. \(\widehat {{A_3}} = \widehat {{B_1}}\)
D. \(\widehat {{A_3}} = \widehat {{B_3}}\)
Phương pháp giải:
Tính chất 2 đường thẳng song song
Lời giải chi tiết:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}}; \widehat {{A_3}} = \widehat {{B_3}}\) ( 2 góc đồng vị);
\(\widehat {{A_3}} = \widehat {{B_1}}\) ( 2 góc so le trong)
Vậy khẳng định A sai; B,C,D đúng
Chọn A
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
A. \(\widehat {BOM}\) và \(\widehat {CON}\) | B.\(\widehat {AOB}\) và \(\widehat {AON}\) |
C. \(\widehat {AOM}\) và \(\widehat {CON}\) | D. \(\widehat {COM}\) và \(\widehat {CON}\). |
Phương pháp giải:
+ Vẽ hình
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Lời giải chi tiết:
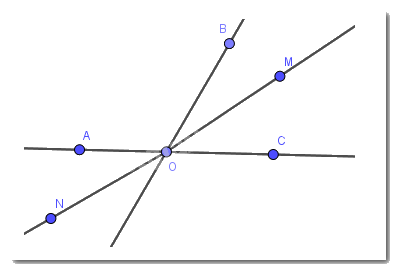
Cặp góc đối đỉnh là cặp góc \(\widehat {AOM}\) và \(\widehat {CON}\)
Chọn C
Trong các khẳng định sau, khẳng định nào đúng?
A. Hai góc bằng nhau thì đối đỉnh;
B. Hai góc không đối đỉnh thì không bằng nhau;
C. Hai góc đối đỉnh thì bằng nhau;
D. Cả ba khẳng định trên đều đúng.
Phương pháp giải:
Tính chất 2 góc đối đỉnh
Lời giải chi tiết:
A. Sai vì 2 góc bằng nhau chưa chắc đã đối đỉnh
B. Sai vì 2 góc không đối đỉnh cũng có thể bằng nhau (chỉ cần số đo của chúng bằng nhau)
C. Đúng
Chọn C
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc đó là \({65^0}\). Khi đó số đo của ba góc còn lại là:
A.\({65^0};{110^0};{120^0};\) | B. \({65^0};{65^0};{115^0};\) |
C. \({115^0};{115^0};{50^0};\) | D. \({65^0};{115^0};{115^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
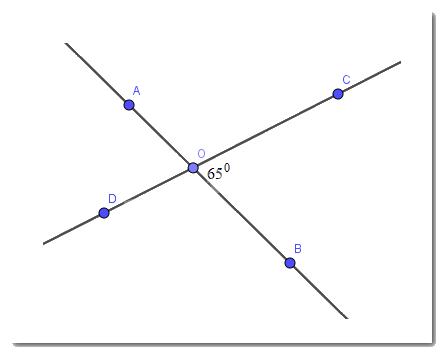
Giả sử hai đường thẳng AB và CD cắt nhau tại O, tạo ra góc BOC có số đo \(65^0\)
\(\Rightarrow \widehat{AOD}=\widehat{BOC}=65^0\) (2 góc đối đỉnh)
\(\widehat{AOB}+\widehat{BOC}=180^0\) (2 góc kề bù) nên \(\widehat{AOB}=180^0-65^0=115^0\)
\(\widehat{COD}=\widehat{AOB}=115^0\) (2 góc đối đỉnh)
Chọn D
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
A.\({70^0};{70^0};{70^0};{110^0}\) | B. \({60^0};{120^0};{120^0};{120^0};\) |
C. \({80^0};{50^0};{130^0};{100^0};\) | D. \({90^0};{90^0};{90^0};{90^0}.\) |
Phương pháp giải:
Hai góc đối đỉnh thì bằng nhau
Hai góc kề bù có tổng số đo là 180 độ.
Lời giải chi tiết:
2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
Mà 2 góc đối đỉnh thì bằng nhau
Chọn D
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = {30^0}\). Số đo của góc AOC bằng:
A.\({30^0};\) | B. \({60^0};\) |
C. \({120^0};\) | D. Một kết quả khác. |
Phương pháp giải:
Nếu OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\)
Hai góc đối đỉnh thì bằng nhau
Lời giải chi tiết:
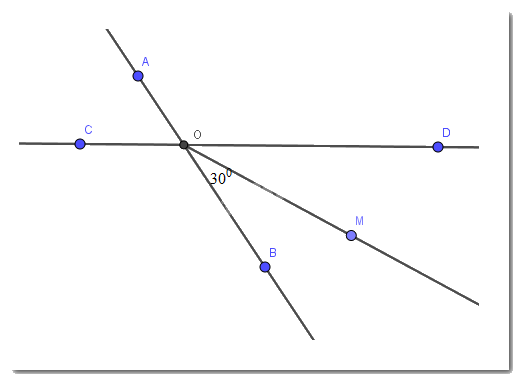
Vì OM là tia phân giác của góc BOD thì \(\widehat{BOM}=\widehat{MOD}=\dfrac{1}{2}.\widehat{BOD}\) nên \(\widehat{BOD}=2. \widehat{BOM}=2.30^0=60^0\)
Ta có: \(\widehat{AOC}=\widehat{BOD}\) ( 2 góc đối đỉnh)
Do đó, \(\widehat{AOC}=60^0\)
Chọn B
Cho hình 3.29.
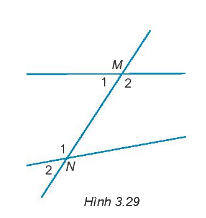
a) Cặp góc so le trong là cặp góc
A.\(\widehat {{M_1}},\widehat {{M_2}};\) | B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
C. \(\widehat {{M_1}},\widehat {{N_2}};\) | D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
b) Cặp góc đồng vị là cặp góc:
A.\(\widehat {{M_1}},\widehat {{M_2}};\) | B. \(\widehat {{M_1}},\widehat {{N_1}};\) |
C. \(\widehat {{M_1}},\widehat {{N_2}};\) | D. \(\widehat {{M_2}},\widehat {{N_1}}.\) |
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt.
Lời giải chi tiết:
a) Chọn D
b) Chọn C
Cho hình 3.30. Cặp góc \(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc:
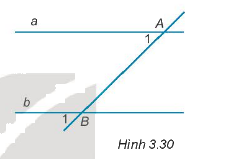
A. So le trong;
B. Đối đỉnh;
C. Đồng vị;
D. Cả ba phương án trên đều sai.
Phương pháp giải:
Nhận biết các góc ở vị trí đặc biệt
Lời giải chi tiết:
\(\widehat {{A_1}};\widehat {{B_1}}\) là cặp góc đồng vị
Chọn C
Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu
A.\(\widehat {{A_1}} = \widehat {{B_2}}\)
B. \(\widehat {{A_2}} = \widehat {{B_3}}\)
C. \(\widehat {{A_3}} = \widehat {{B_2}}\)
D. \(\widehat {{A_3}} = \widehat {{B_1}}\)
Phương pháp giải:
Dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết:
a//b nếu đường thẳng c cắt hai đường thẳng a và b, tạo thành 1 cặp góc so le trong bằng nhau hoặc 1 cặp góc đồng vị bằng nhau.
Xét khẳng định D:
\(\widehat {{A_3}} = \widehat {{B_1}}\)
Mà 2 góc này ở vị trí so le trong
Do đó, a//b
Chọn D
Cho Hình 3.32, biết \(a// b\).
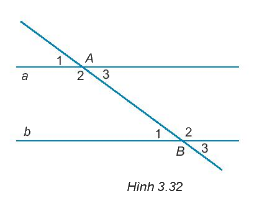
Khẳng định nào sau đây là sai?
A.\(\widehat {{A_1}} > \widehat {{B_1}}\)
B. \(\widehat {{A_2}} = \widehat {{B_2}}\)
C. \(\widehat {{A_3}} = \widehat {{B_1}}\)
D. \(\widehat {{A_3}} = \widehat {{B_3}}\)
Phương pháp giải:
Tính chất 2 đường thẳng song song
Lời giải chi tiết:
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}}; \widehat {{A_3}} = \widehat {{B_3}}\) ( 2 góc đồng vị);
\(\widehat {{A_3}} = \widehat {{B_1}}\) ( 2 góc so le trong)
Vậy khẳng định A sai; B,C,D đúng
Chọn A
Trang 47 và 48 của sách bài tập Toán 7 Kết nối tri thức với cuộc sống tập trung vào các chủ đề quan trọng như biểu thức đại số, tính chất của phép cộng, phép trừ, phép nhân, phép chia số hữu tỉ, và các bài toán liên quan đến ứng dụng thực tế. Việc nắm vững kiến thức và kỹ năng giải các bài tập trắc nghiệm trong hai trang này là nền tảng vững chắc cho việc học tập môn Toán ở các lớp trên.
Nội dung chính của trang 47 và 48 bao gồm:
Để giải các bài tập trắc nghiệm trang 47,48 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Dưới đây là giải chi tiết một số bài tập trắc nghiệm tiêu biểu trên trang 47 và 48:
Cho biểu thức A = 3x + 5y - 2z. Tính giá trị của A khi x = 2, y = -1, z = 3.
Giải:
Thay x = 2, y = -1, z = 3 vào biểu thức A, ta có:
A = 3(2) + 5(-1) - 2(3) = 6 - 5 - 6 = -5
Vậy, giá trị của A là -5.
Tìm x biết: 2(x - 1) + 3 = 7
Giải:
2(x - 1) + 3 = 7
2(x - 1) = 7 - 3
2(x - 1) = 4
x - 1 = 4 : 2
x - 1 = 2
x = 2 + 1
x = 3
Vậy, x = 3.
Để củng cố kiến thức và kỹ năng giải bài tập, bạn có thể luyện tập thêm với các bài tập sau:
Việc giải các bài tập trắc nghiệm trang 47,48 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng với hướng dẫn chi tiết và các phương pháp giải bài tập hiệu quả, bạn sẽ tự tin hơn trong việc giải quyết các bài toán và đạt kết quả tốt trong học tập.