Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 11 trang 70 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những em mới làm quen với chương trình học mới.
Bài viết này sẽ giúp bạn nắm vững kiến thức, phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán 7.
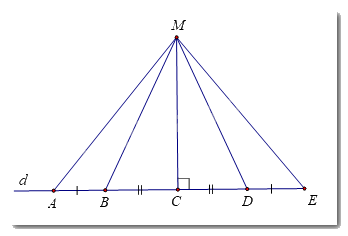
Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
Đề bài
Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a)\(\Delta MBC = \Delta MDC,\Delta MAC = \Delta MEC\)
b)\(\Delta MAB = \Delta MED\)
Phương pháp giải - Xem chi tiết
-Chứng minh:
\(\begin{array}{l}\Delta MBC = \Delta MDC\left( {c - g - c} \right),\\\Delta MAC = \Delta MEC\left( {c - g - c} \right)\end{array}\)
-Áp dụng kết quả ý a, chứng minh b) \(\Delta MAB = \Delta MED\left( {c - c - c} \right)\)
Lời giải chi tiết
a)
-Xét \(\Delta MBC\) và \(\Delta MDC\)có:
\(\begin{array}{l}\widehat {MCB} = \widehat {BCD} = {90^0}\\BC = CD\left( {gt} \right)\\MC:chung\\ \Rightarrow \Delta MBC = \Delta MDC\left( {c - g - c} \right)\\ \Rightarrow MB = MD\left( {ctu} \right)\end{array}\)
-Xét \(\Delta MAC\) và \(\Delta MEC\)có:
\(\begin{array}{l}\widehat {MCA} = \widehat {MCE} = {90^0}\\MC:chung\\\left\{ \begin{array}{l}AC = AB + BC\\EC = DE + CD\end{array} \right.\\Do\,AB = DE;BC = CD\left( {gt} \right)\\ \Rightarrow AC = EC\\ \Rightarrow \Delta MAC = \Delta MEC\left( {c - g - c} \right)\\ \Rightarrow MA = ME\left( {ctu} \right)\end{array}\)
b)
Xét \(\Delta MAB\)và \(\Delta MED\)có:
MA = ME (cmt)
MB = MD (cmt)
AB = ED (gt) \( \Rightarrow \Delta MAB = \Delta MED\left( {c - c - c} \right)\)
Bài 11 trang 70 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số hữu tỉ, biểu diễn số hữu tỉ trên trục số, và các tính chất của số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Bài 11 bao gồm các dạng bài tập sau:
Thực hiện phép tính:
Giải:
So sánh các số hữu tỉ:
Giải:
Để học tốt môn Toán 7 - Kết nối tri thức, bạn nên:
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải Bài 11 trang 70 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!