Bài 9.14 trang 55 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này thường yêu cầu học sinh phải phân tích hình vẽ, xác định các góc so le trong, đồng vị, và góc trong cùng phía để đưa ra kết luận về mối quan hệ giữa các đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 9.14 trang 55 SBT Toán 7 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho
Đề bài
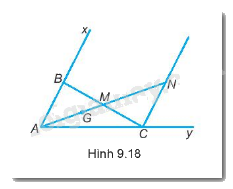
Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho \(AM = \dfrac{3}{2}AG;AN = 2AM\). Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B.
a)Chứng minh hai tam giác ABM và NCM bằng nhau, từ đó suy ra AM là đường trung tuyến của tam giác ABC.
b) Chứng minh rằng G là trọng tâm của tam giác ABC vừa dựng được.
Phương pháp giải - Xem chi tiết
a)Chứng minh: \(\Delta ABM = \Delta NCM\left( {g - c - g} \right)\)
b)Chứng minh: \(AG = \dfrac{2}{3}AM\).
Lời giải chi tiết
a)
Xét \(\Delta ABM\)và \(\Delta NCM\) có:
\(\widehat {MAB} = \widehat {MNC}\)(2 góc so le trong NC // Ax)
\(\widehat {AMB} = \widehat {NMC}\)(2 góc đối đỉnh)
AN = 2AM =>AM = NM
\( \Rightarrow \Delta ABM = \Delta NCM\left( {g - c - g} \right)\)
\( \Rightarrow MB = MC\)(cạnh tương ứng)
\( \Rightarrow M\)là trung điểm của BC
Vậy AM là đường trung tuyến của tam giác ABC.
b)
Ta có: Điểm G nằm trên đường trung tuyến AM của tam giác ABC
\(AM = \dfrac{3}{2}AG \Rightarrow AG = \dfrac{2}{3}AM\)
Vậy G là trọng tâm tam giác ABC.
Bài 9.14 trang 55 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để chứng minh hai đường thẳng song song. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa và tính chất của các loại góc: góc so le trong, góc đồng vị, góc trong cùng phía.
Bài tập thường cho một hình vẽ với hai đường thẳng bị cắt bởi một đường thẳng thứ ba. Học sinh cần xác định các góc và sử dụng các tính chất của các góc để chứng minh hai đường thẳng đó song song. Ví dụ, nếu góc so le trong bằng nhau, hoặc góc đồng vị bằng nhau, hoặc góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Đề bài: Cho hình vẽ, biết ∠A = 60°. Chứng minh AB // CD.
Giải:
Ngoài các góc so le trong, đồng vị, và góc trong cùng phía, còn có các loại góc khác như góc kề bù, góc nhọn, góc tù. Việc nắm vững các loại góc và tính chất của chúng là rất quan trọng để giải các bài tập về đường thẳng song song và các bài tập hình học khác.
Để củng cố kiến thức và kỹ năng giải bài tập về các góc tạo bởi đường thẳng cắt đường thẳng, học sinh có thể làm thêm các bài tập tương tự trong sách bài tập Toán 7 Kết nối tri thức hoặc các tài liệu tham khảo khác.
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 7 Kết nối tri thức và các chương trình Toán khác. Chúng tôi luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả, giúp các em học sinh học toán một cách dễ dàng và thú vị.
| Dấu hiệu | Mô tả |
|---|---|
| Hai đường thẳng song song | Nếu hai đường thẳng phân biệt có hai góc so le trong bằng nhau. |
| Hai đường thẳng song song | Nếu hai đường thẳng phân biệt có hai góc đồng vị bằng nhau. |
| Hai đường thẳng song song | Nếu hai đường thẳng phân biệt có hai góc trong cùng phía bù nhau. |
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 7 Kết nối tri thức. Chúc các em học tốt!