Chào mừng các em học sinh đến với lời giải chi tiết Bài 13 trang 70 Sách Bài Tập Toán 7 - Kết Nối Tri Thức. Bài viết này sẽ cung cấp đáp án đầy đủ, dễ hiểu, cùng với phương pháp giải bài tập một cách hiệu quả.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho bốn điểm A, B, C và D như Hình 2. Biết rằng
Đề bài
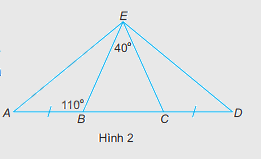
Cho bốn điểm A, B, C và D như Hình 2. Biết rằng \(\widehat {BEC} = {40^0};\widehat {EBA} = {110^0};AB = DC\). Chứng minh rằng:
a) Tam giác BEC cân tại đỉnh E.
b) EA = ED.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\widehat {EBC} = \widehat {ECB} = {70^0}\)
b) Chứng minh: \(\Delta ABE = \Delta DCE\left( {c - g - c} \right)\).
Lời giải chi tiết
a) Ta có: \(\widehat {ABE} + \widehat {EBC} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l}{110^0} + \widehat {EBC} = {180^0}\\ \text{nên}\,\widehat {EBC} = {180^0} - {110^0} = {70^0}\end{array}\)
Xét tam giác EBC: \(\widehat E + \widehat B + \widehat C = {180^0}\) (Tổng ba góc trong tam giác)
\(\begin{array}{l} {40^0} + {70^0} + \widehat C = {180^0}\\ \text{nên}\,\widehat C = {180^0} - {110^0} = {70^0}\end{array}\)
suy ra \(\widehat {EBC} = \widehat {ECB} = {70^0}\)
nên \(\Delta EBC\) cân tại E
do đó \( EB = EC\)
b) Chứng minh EA = ED
Ta có:
\(\begin{array}{l}\widehat {ECD} = {180^0} - \widehat {ECB} = {180^0} - {70^0} = {110^0} \end{array}\)
nên \(\widehat {ABE} = \widehat {DCE}\)
Xét \(\Delta ABE\)và có:
\(\begin{array}{l}BE = CE\left( {cmt} \right)\\\widehat {ABE} = \widehat {DCE}\left( {cmt} \right)\\AB = DC\left( {gt} \right)\\ \text{nên}\,\Delta ABE = \Delta DCE\left( {c - g - c} \right)\\ \text{suy ra}\,AE = DE\end{array}\)
Bài 13 trang 70 Sách Bài Tập Toán 7 - Kết Nối Tri Thức tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, đặc biệt là các phép toán cộng, trừ, nhân, chia đa thức. Mục tiêu chính của bài tập là rèn luyện kỹ năng biến đổi biểu thức, đơn giản hóa biểu thức và tìm giá trị của biểu thức khi biết giá trị của biến.
Bài 13 bao gồm một số câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để tính giá trị của biểu thức tại một giá trị cụ thể của biến, ta chỉ cần thay giá trị của biến vào biểu thức và thực hiện các phép toán. Ví dụ:
Cho biểu thức A = 2x + 3y. Tính giá trị của A khi x = 1 và y = -1.
Giải:
A = 2(1) + 3(-1) = 2 - 3 = -1
Để rút gọn biểu thức đại số, ta sử dụng các quy tắc về phép toán cộng, trừ, nhân, chia đa thức, đồng thời áp dụng các hằng đẳng thức đại số. Ví dụ:
Rút gọn biểu thức B = (x + 2)(x - 2) + x2
Giải:
B = x2 - 4 + x2 = 2x2 - 4
Để tìm x để biểu thức có giá trị bằng 0, ta giải phương trình với ẩn x. Ví dụ:
Tìm x để biểu thức C = 3x - 6 = 0
Giải:
3x - 6 = 0 => 3x = 6 => x = 2
Để chứng minh đẳng thức, ta biến đổi một vế của đẳng thức để được vế còn lại. Ví dụ:
Chứng minh đẳng thức (x + y)2 = x2 + 2xy + y2
Giải:
(x + y)2 = (x + y)(x + y) = x2 + xy + yx + y2 = x2 + 2xy + y2
Việc giải bài tập Toán 7 không chỉ giúp học sinh củng cố kiến thức đã học mà còn rèn luyện kỹ năng tư duy logic, khả năng giải quyết vấn đề và sự kiên trì. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết Bài 13 trang 70 Sách Bài Tập Toán 7 - Kết Nối Tri Thức một cách hiệu quả. Chúc các em học tập tốt!