Bài 9.17 trang 55 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này thường yêu cầu học sinh phải phân tích hình vẽ, xác định các góc so le trong, đồng vị, và góc trong cùng phía để suy luận và tìm ra kết quả.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.17, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Tam giác ABC có AD, BE là hai đường phân giác và
Đề bài
Tam giác ABC có AD, BE là hai đường phân giác và \(\widehat {BAC} = {120^0}\). Chứng minh rằng DE là tia phân giác của góc ADC.
Phương pháp giải - Xem chi tiết
- Gọi Ax là tia đối của tia AB
-Chứng minh: \(\widehat {BAD} = \widehat {DAC} = \widehat {CAx}\)
- Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\)
-Áp dụng điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của của góc đó.
Lời giải chi tiết
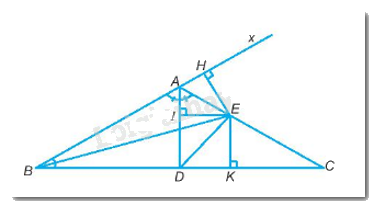
Gọi Ax là tia đối của tia AB \(\widehat {CAx} = {180^0} - \widehat {BAC} = {180^0} - {120^0} = {60^0}\) (2 góc kề bù)
AD là phân giác góc BAC
\( \Rightarrow \widehat {BAD} = \widehat {DAC} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\)
\( \Rightarrow \widehat {BAD} = \widehat {DAC} = \widehat {CAx}\)
Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\)
Ta có:
EH = EK (vì BE là phân giác góc ABC)
EH = EI (vì AE là phân giác góc DAx)
\( \Rightarrow EK = EI\)
Vậy E nằm trên tia phân giác của góc ADC.
Bài 9.17 thuộc chương 3: Các góc tạo bởi đường thẳng cắt đường thẳng của sách bài tập Toán 7 Kết nối tri thức với cuộc sống. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về các cặp góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Cho hình vẽ sau (hình vẽ cần được mô tả chi tiết, ví dụ: hai đường thẳng a và b cắt nhau tại điểm O, có các góc được đánh số từ 1 đến 8). Yêu cầu của bài tập thường là:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
(Phần này sẽ trình bày lời giải chi tiết cho từng yêu cầu của bài tập, kèm theo hình vẽ minh họa nếu cần thiết. Ví dụ:)
a) Tìm các cặp góc so le trong:
Các cặp góc so le trong là: ∠1 và ∠5; ∠2 và ∠6; ∠3 và ∠7; ∠4 và ∠8.
b) Tìm các cặp góc đồng vị:
Các cặp góc đồng vị là: ∠1 và ∠3; ∠2 và ∠4; ∠5 và ∠7; ∠6 và ∠8.
c) Tìm các cặp góc trong cùng phía:
Các cặp góc trong cùng phía là: ∠1 và ∠6; ∠2 và ∠5; ∠3 và ∠8; ∠4 và ∠7.
d) Chứng minh ∠1 = ∠5:
Vì ∠1 và ∠5 là hai góc so le trong nên ∠1 = ∠5 (theo tính chất hai đường thẳng song song).
Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xét một ví dụ khác. Giả sử cho hai đường thẳng a và b cắt nhau tại điểm O, và ∠1 = 60°. Hãy tìm số đo của các góc còn lại.
Lời giải:
Để củng cố kiến thức, các em học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 7 Kết nối tri thức với cuộc sống. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 9.17 trang 55 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh hiểu rõ và vận dụng các kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.