Bài 4.21 trang 60 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tam giác cân, góc ở đáy và góc đỉnh. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán thực tế liên quan đến tam giác cân.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.21 trang 60 sách bài tập Toán 7 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Đề bài
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
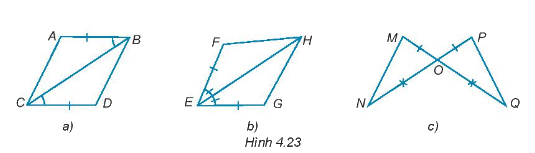
Phương pháp giải - Xem chi tiết
Nếu 2 cạnh và góc xem giữa của tam giác này bằng 2 cạnh và góc xem giữa của tam giác kia thì 2 tam giác đó bằng nhau.
Lời giải chi tiết
a) Xét \(\Delta ABC\) và \(\Delta DCB\) có:
AB = DC
\(\widehat {ABC} = \widehat {DCB}\)
BC: Cạnh chung
Suy ra \(\Delta ABC = \Delta DCB\left( {c - g - c} \right)\)
b) Xét \(\Delta HEF\) và \(\Delta HEG\) có:
EF = EG
\(\widehat {FEH} = \widehat {GEH}\)
EH: Cạnh chung
Suy ra \(\Delta HEF = \Delta HEG\left( {c - g - c} \right)\)
c) Xét \(\Delta MON\) và \(\Delta POQ\) có:
OM = OP
ON = OQ
\(\widehat {MON} = \widehat {POQ}\)( 2 góc đối đỉnh)
Suy ra \(\Delta MON = \Delta POQ\left( {c - g - c} \right)\)
Bài 4.21 trang 60 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về tam giác cân để giải quyết một bài toán hình học cụ thể. Để giải bài này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm cơ bản về tam giác cân:
Đề bài: (Giả sử đề bài là: Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC. Chứng minh AD là đường phân giác của góc BAC.)
a. Phân tích bài toán:
Để chứng minh AD là đường phân giác của góc BAC, ta cần chứng minh góc BAD bằng góc CAD. Ta có thể sử dụng các tính chất của tam giác cân và trung điểm để chứng minh điều này.
b. Chứng minh:
Việc hiểu rõ các tính chất của tam giác cân là rất quan trọng để giải quyết bài toán này. Đường trung tuyến trong tam giác cân không chỉ là đường nối trung điểm của một cạnh với đỉnh đối diện mà còn đóng vai trò là đường cao và đường phân giác, giúp chúng ta đơn giản hóa quá trình chứng minh.
Ngoài bài 4.21, sách bài tập Toán 7 Kết nối tri thức còn có nhiều bài tập tương tự về tam giác cân. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập về tam giác cân một cách hiệu quả, bạn nên:
Để củng cố kiến thức về tam giác cân, bạn có thể luyện tập thêm các bài tập sau:
Bài 4.21 trang 60 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về tam giác cân và các tính chất của nó. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.