Bài 3.19 trang 42 sách bài tập Toán 7 thuộc chương 3: Các góc và đường thẳng song song của chương trình Toán 7 Kết nối tri thức với cuộc sống. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, góc đồng vị, góc trong cùng phía để chứng minh tính chất của hai đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.19 trang 42, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Vẽ lại hình 3.20 vào vở.
Đề bài
Vẽ lại hình 3.20 vào vở.
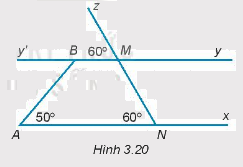
a) Giải thích tại sao \(Ax\parallel By.\)
b) Tính số đo góc \(ABy'\).
c) Tính số đo góc ABM.
Phương pháp giải - Xem chi tiết
a) Chỉ ra 2 góc đồng vị bằng nhau
b) Chỉ ra 2 góc so le trong bằng nhau
c) \(\widehat {ABM} + \widehat {ABy'} = {180^0}\)
Lời giải chi tiết
a)
Ta có: \(\widehat {BMz} = \widehat {ANM}\left( { = {{60}^0}} \right)\)
Mà hai góc ở vị trí đồng vị nên \(Ax\parallel By\)(dấu hiệu nhận biết 2 đường thẳng song song).
b)
Ta có: \(Ax\parallel By\)\( \Rightarrow \widehat {ABy'} = \widehat {BAN}\)(2 góc so le trong)
Do đó \(\widehat {ABy'} = {50^0}\).
c)
Ta có: \(\widehat {ABM} + \widehat {ABy'} = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ABM} + {50^0} = {180^0}\\ \Rightarrow \widehat {ABM} = {180^0} - {50^0}\\ \Rightarrow \widehat {ABM} = {130^0}\end{array}\)
Bài 3.19 yêu cầu chúng ta chứng minh hai đường thẳng song song dựa trên các điều kiện về góc. Để giải bài này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài tập 3.19: Cho hình vẽ (hình vẽ cần được mô tả chi tiết, ví dụ: a // b, góc A = 60 độ, góc B = 120 độ). Chứng minh a song song với b.
Lời giải:
Trong hình vẽ, ta thấy góc A và góc B là hai góc trong cùng phía. Nếu chúng ta chứng minh được góc A + góc B = 180 độ thì ta có thể kết luận a song song với b.
Ta có: góc A = 60 độ và góc B = 120 độ. Do đó, góc A + góc B = 60 độ + 120 độ = 180 độ.
Vậy, a song song với b (theo dấu hiệu hai góc trong cùng phía bù nhau).
Ví dụ minh họa khác:
Giả sử hình vẽ có a cắt b tại điểm O, và góc AOC = 70 độ, góc BOD = 110 độ. Chứng minh a song song với b.
Lời giải:
Ta có: góc AOC và góc BOD là hai góc đồng vị. Nếu chúng ta chứng minh được góc AOC = góc BOD thì ta có thể kết luận a song song với b.
Tuy nhiên, trong trường hợp này, góc AOC = 70 độ và góc BOD = 110 độ, nên góc AOC ≠ góc BOD. Do đó, chúng ta không thể kết luận a song song với b dựa trên dấu hiệu hai góc đồng vị bằng nhau.
Thay vào đó, ta có thể xét góc AOC và góc BOx (kề bù với góc BOD). Khi đó, góc BOx = 180 độ - 110 độ = 70 độ.
Vì góc AOC = góc BOx = 70 độ, nên a song song với b (theo dấu hiệu hai góc so le trong bằng nhau).
Lưu ý khi giải bài tập về đường thẳng song song:
Bài tập tương tự:
Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh đã hiểu rõ cách giải bài 3.19 trang 42 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống. Chúc các em học tập tốt!