Bài 10.6 trang 63 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học toán lớp 7. Bài tập này giúp học sinh rèn luyện kỹ năng giải toán về các góc và đường thẳng song song.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
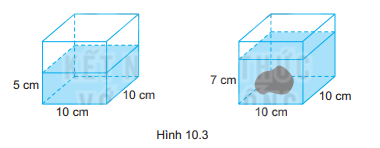
Bạn Hà có một bể cá có dạng hình lập phương có độ dài cạnh 10 cm. Ban đầu nước trong bể có độ cao 5 cm. Bạn Hà bỏ thêm vào trong bể một hòn đá trang trí chìm trong nước thì nước trong bể có độ cao 7cm (H.10.3). Hỏi hòn đá bạn Hà bỏ vào bể có thể tích bao nhiêu cm3 ?
Đề bài
Bạn Hà có một bể cá có dạng hình lập phương có độ dài cạnh 10 cm. Ban đầu nước trong bể có độ cao 5 cm. Bạn Hà bỏ thêm vào trong bể một hòn đá trang trí chìm trong nước thì nước trong bể có độ cao 7cm (H.10.3). Hỏi hòn đá bạn Hà bỏ vào bể có thể tích bao nhiêu cm3 ?
Phương pháp giải - Xem chi tiết
-Tính tổng thể tích của nước và hòn đá.
-Tính thể tích nước trong bể ban đầu.
Lời giải chi tiết
Tổng thể tích của nước và hòn đá là:
\({V_1} = 10 \cdot 10 \cdot 7 = 700\left( {c{m^3}} \right)\)
Thể tích nước trong bể ban đầu là:
\({V_2} = 10 \cdot 10 \cdot 5 = 500\left( {c{m^3}} \right)\)
Thể tích hòn đá là:
\(V = {V_1} - {V_2} = 700 - 500 = 200\left( {c{m^3}} \right)\)
Bài 10.6 trang 63 Sách Bài Tập Toán 7 - Kết Nối Tri Thức yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bài tập bằng cách:
(Giả sử đề bài là: Cho hình vẽ, biết góc A1 = 60 độ. Tính các góc còn lại.)
Giải:
Vì góc A1 và góc B1 là hai góc so le trong nên góc B1 = góc A1 = 60 độ.
Vì góc A1 và góc A2 là hai góc kề bù nên góc A2 = 180 độ - góc A1 = 180 độ - 60 độ = 120 độ.
Vì góc A2 và góc B2 là hai góc đồng vị nên góc B2 = góc A2 = 120 độ.
Vì góc B1 và góc B3 là hai góc kề bù nên góc B3 = 180 độ - góc B1 = 180 độ - 60 độ = 120 độ.
Vậy, các góc còn lại là: góc B1 = 60 độ, góc A2 = 120 độ, góc B2 = 120 độ, góc B3 = 120 độ.
Ngoài bài 10.6 trang 63, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về các góc và đường thẳng song song. Để giải các bài tập này một cách hiệu quả, bạn có thể áp dụng các mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 10.6 trang 63 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc và đường thẳng song song. Bằng cách nắm vững kiến thức, phân tích đề bài và áp dụng các mẹo giải, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.