Bài 10.14 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học toán lớp 7. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
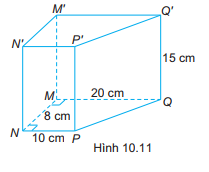
Cho hình lăng trụ đứng MNPQ.M’N’P’Q’ có đáy MNPQ là hình thang vuông tại M và N. Kích thước các cạnh như Hình 10.11. Tính thể tích hình lăng trụ.
Đề bài
Cho hình lăng trụ đứng MNPQ.M’N’P’Q’ có đáy MNPQ là hình thang vuông tại M và N. Kích thước các cạnh như Hình 10.11. Tính thể tích hình lăng trụ.
Phương pháp giải - Xem chi tiết
-Tính diện tích đáy là hình thang vuông.
-Tính V = Sđáy . h.
Lời giải chi tiết
Diện tích hình thang vuông MNPQ là:
\(S = \dfrac{1}{2}\left( {MQ + NP} \right).MN = \dfrac{1}{2}\left( {20 + 10} \right).8 = 120\left( {c{m^2}} \right)\)
Thể tích của hình lăng trụ đứng MNPQ.M’N’P’Q’ là:
V = S . h = 120 . 15 = 1 800 (cm3).
Bài 10.14 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức yêu cầu học sinh phân tích hình vẽ và áp dụng các tính chất của góc so le trong, góc đồng vị, góc trong cùng phía để tính toán các góc chưa biết. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, vẽ hình (nếu cần) và xác định các yếu tố đã biết và yếu tố cần tìm. Trong bài 10.14, chúng ta thường được cho một số góc và yêu cầu tính các góc còn lại. Việc lập kế hoạch giải bài tập sẽ giúp chúng ta tiếp cận vấn đề một cách có hệ thống và tránh sai sót.
Dưới đây là lời giải chi tiết cho bài 10.14 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức. (Lưu ý: Vì đề bài cụ thể của bài 10.14 có thể khác nhau tùy theo phiên bản sách, chúng ta sẽ đưa ra một ví dụ minh họa và hướng dẫn giải chung):
Ví dụ: Cho hình vẽ, biết góc A = 60 độ. Tính góc B.
(Hình vẽ minh họa với hai đường thẳng cắt nhau và các góc A, B được đánh dấu)
Ngoài bài 10.14, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, chúng ta cần:
Để củng cố kiến thức và nâng cao kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập khác trong sách bài tập và các tài liệu tham khảo. Bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín như giaitoan.edu.vn.
Bài 10.14 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về các góc tạo bởi đường thẳng cắt đường thẳng. Bằng cách nắm vững kiến thức cơ bản, phân tích đề bài một cách cẩn thận và luyện tập thường xuyên, bạn sẽ có thể giải quyết bài tập này một cách dễ dàng và tự tin.
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải bài 10.14 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức. Chúc bạn học tốt!