Bài 4.41 trang 68 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính toán và chứng minh các mối quan hệ giữa các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.41 trang 68 SBT Toán 7 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
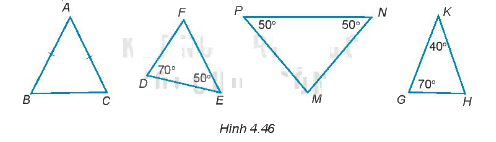
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?
Đề bài
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?
Phương pháp giải - Xem chi tiết
Chỉ ra 2 cạnh bên bằng nhau hoặc 2 góc ở đáy bằng nhau.
Lời giải chi tiết
+) Xét \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) cân tại đỉnh A
+) Xét \(\Delta DEF\) có:
\(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)(Định lí tổng 3 góc trong tam giác)
\(\Rightarrow 70^0+50^0+\widehat{F}=180^0\)
\(\Rightarrow \widehat{F}=60^0\)
Ta thấy \(\Delta DEF\) không có cặp góc nào bằng nhau nên không là tam giác cân.
+) Xét \(\Delta MNP\) có \(\widehat N = \widehat P (= {50^0})\) nên \(\Delta MNP\) cân tại đỉnh M
+) Xét \(\Delta KGH\) có:
\(\widehat{K}+\widehat{G}+\widehat{H}=180^0\)(Định lí tổng 3 góc trong tam giác)
\(\widehat H = {180^0} - \widehat K - \widehat G = {180^0} - {40^0} - {70^0} = {70^0} \)
Ta được \(\Delta KGH\) có \(\widehat H = \widehat G(=70^0)\) nên \(\Delta KGH\) cân tại đỉnh K
Bài 4.41 trang 68 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin đã cho. Xác định rõ các yếu tố cần tìm và các mối quan hệ giữa chúng. Sau đó, chúng ta sẽ tìm ra hướng giải quyết phù hợp bằng cách vận dụng các kiến thức đã học.
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình vẽ, biết góc AOB = 40 độ. Tính góc COD.)
Giải:
Ví dụ: (Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết.)
Giải thích: Vì góc AOB và góc COD là hai góc đối đỉnh nên góc COD = góc AOB = 40 độ.
Ngoài bài 4.41 trang 68, sách bài tập Toán 7 Kết nối tri thức còn có nhiều bài tập tương tự về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, hàng hải, và thiên văn học. Ví dụ, trong kiến trúc, các kiến trúc sư sử dụng kiến thức này để thiết kế các tòa nhà có góc cạnh đẹp mắt và đảm bảo tính thẩm mỹ. Trong hàng hải, các thủy thủ sử dụng kiến thức này để xác định phương hướng và vị trí của tàu.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em học sinh có thể tự giải các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và dễ hiểu bài 4.41 trang 68 SBT Toán 7 Kết nối tri thức, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!