Bài 9.23 trang 60 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các góc so le trong, đồng vị, trong cùng phía và góc kề bù.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.23, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho D là một điểm bên trong tam giác ABC. Chứng minh:
Đề bài
Cho D là một điểm bên trong tam giác ABC. Chứng minh:
a)\(\widehat {BDC} > \widehat {BAC}\)
b) BD + DC < AB + AC
Phương pháp giải - Xem chi tiết
a)
- Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.
-Áp dụng tính chất góc ngoài của tam giác
b)
- Gọi E là giao điểm của BD và AC. Ta có:
AB + AC = AB + (AE + EC) = (AB + AE) + EC
-Áp dụng các bất đẳng thức cho tam giác: ABE, DEC
Lời giải chi tiết
a)
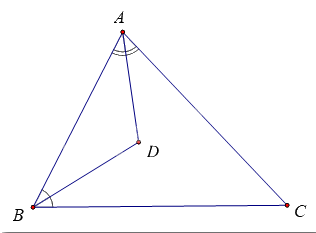
Tia AD chia góc A thành góc A1 và góc A2, chia góc BDC thành góc D1 và góc D2.
Góc D1 là góc ngoài tại đỉnh D của tam giác ABD nên:
\(\widehat {{D_1}} > \widehat {{A_1}}\)
Góc D2 là góc ngoài tại đỉnh D của tam giác ADC nên:
\(\widehat {{D_2}} > \widehat {{A_2}}\)
\( \Rightarrow \widehat D = \widehat {{D_1}} + \widehat {{D_2}} > \widehat {{A_1}} + \widehat {{A_2}} = \widehat A\)
b)
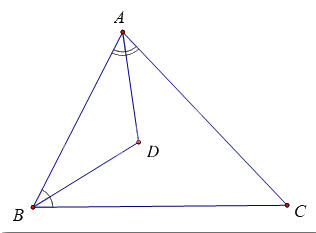
Gọi E là giao điểm của BD và AC. Ta có:
AB + AC = AB + (AE + EC) = (AB + AE) + EC
Mà: AB + AE > BE (bất đẳng thức trong tam giác ABE)
=>(AB + AE) + EC > BE + EC = (BD + DE) + EC = BD + (DE + EC)
Mà DE + EC > DC (bất đẳng thức trong tam giác DEC)
=>AB + AC > BD + DC.
Bài 9.23 sách bài tập Toán 7 Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết một bài toán thực tế. Dưới đây là lời giải chi tiết và các kiến thức liên quan:
Cho hình vẽ sau (hình vẽ cần được mô tả chi tiết, ví dụ: a // b, c cắt a và b tại A và B, góc A1 = 60 độ). Tìm số đo của các góc còn lại trong hình.
Để giải bài toán này, chúng ta cần sử dụng các kiến thức sau:
Giải:
Trong quá trình giải bài 9.23, việc xác định đúng các cặp góc so le trong, đồng vị, trong cùng phía là rất quan trọng. Việc hiểu rõ mối quan hệ giữa các góc này sẽ giúp học sinh dễ dàng tìm ra đáp án chính xác.
Để củng cố kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng, các em có thể tự giải các bài tập tương tự. Ví dụ:
Khi giải các bài tập về góc, các em nên:
Bài 9.23 trang 60 sách bài tập Toán 7 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh hiểu rõ và vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với lời giải chi tiết và các kiến thức liên quan được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!