Bài 3.12 trang 39 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về số hữu tỉ vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.12 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
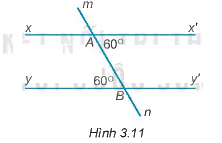
Vẽ lại hình 3.11 vào vở rồi giải thích tại sao xx’ // yy’.
Đề bài
Vẽ lại hình 3.11 vào vở rồi giải thích tại sao xx’ // yy’.
Phương pháp giải - Xem chi tiết
Nếu hai góc so le trong bằng nhau thì hai đường thẳng song song.
Lời giải chi tiết
Ta có: \(\widehat {x'AB} = \widehat {ABy} = {60^0}\)
Mà hai góc ở vị trí so le trong nên \(xx'\parallel yy'\) (dấu hiệu nhận biết hai đường thẳng song song).
Bài 3.12 thuộc chương 1: Các số hữu tỉ của sách bài tập Toán 7 Kết nối tri thức. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về số hữu tỉ, bao gồm:
Bài 3.12 thường yêu cầu học sinh thực hiện các phép toán trên số hữu tỉ, hoặc áp dụng kiến thức về số hữu tỉ để giải quyết các bài toán có tính ứng dụng cao. Dạng bài tập có thể bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích và giải chi tiết từng phần của bài tập. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa.)
Ví dụ 1: Tính giá trị của biểu thức (1/2) + (2/3) - (1/6).
Giải:
Kết luận: Giá trị của biểu thức (1/2) + (2/3) - (1/6) là 1.
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, học sinh có thể tự giải các bài tập tương tự sau:
Khi giải bài tập về số hữu tỉ, học sinh cần lưu ý một số điều sau:
Bài 3.12 trang 39 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về số hữu tỉ. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin hơn trong quá trình học tập.