Bài 10.15 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học toán lớp 7. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp chữ nhật có kích thước như trong Hình 10.12. Tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.
Đề bài
Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp chữ nhật có kích thước như trong Hình 10.12. Tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.
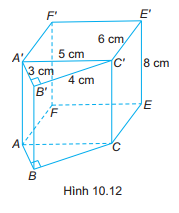
Phương pháp giải - Xem chi tiết
-Tính thể tích hình lăng trụ đứng ABC.A’B’C.
-Tính thể tích hình hộp chữ nhật ACEF.A’C’E’F’.
Lời giải chi tiết
Thể tích hình lăng trụ đứng ABC.A’B’C là:
\({V_1} = S.h = \left( {\dfrac{1}{2} \cdot 3 \cdot 4} \right) \cdot 8 = 48\left( {c{m^3}} \right).\)
Thể tích hình hộp chữ nhật ACEF.A’C’E’F’ là:
\({V_2} = 5 \cdot 6 \cdot 8 = 240\left( {c{m^3}} \right).\)
Thể tích hình lăng trụ đứng ABCEF.A’B’C’E’F’ là:
\(V = {V_1} + {V_2} = 48 + 240 = 288\left( {c{m^3}} \right)\).
Bài 10.15 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài toán ứng dụng thực tế về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Trước khi đi vào giải bài tập, chúng ta cần phân tích đề bài một cách cẩn thận. Đề bài thường yêu cầu chúng ta tìm một góc nào đó dựa trên các thông tin đã cho về các góc khác. Việc đọc kỹ đề bài và vẽ hình minh họa sẽ giúp chúng ta hiểu rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài tập 10.15. (Vì đề bài cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài toán tương tự.)
Ví dụ: Cho hình vẽ, biết góc A1 = 60 độ. Tính các góc A2, B1, B2, B3, B4.
Giải:
Để giải các bài tập về góc tạo bởi đường thẳng cắt đường thẳng, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức về bài tập 10.15, bạn có thể làm thêm một số bài tập luyện tập sau:
Bài 10.15 trang 65 Sách Bài Tập Toán 7 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các góc tạo bởi đường thẳng cắt đường thẳng. Bằng cách nắm vững các kiến thức và áp dụng các mẹo giải bài tập, các em học sinh có thể tự tin giải quyết các bài toán tương tự.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ học tập tốt môn Toán 7. Chúc các em thành công!