Bài 3.35 trang 49 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính toán và chứng minh các mối quan hệ giữa các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.35 trang 49 sách bài tập Toán 7 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình 3.35. Biết CN là tia phân giác của góc ACM.
Đề bài
Cho hình 3.35. Biết CN là tia phân giác của góc ACM.
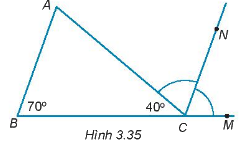
a) Chứng minh rằng \(CN//AB\).
b) Tính số đo của góc A.
Phương pháp giải - Xem chi tiết
a)
- Tính góc ACM (kề bù với góc ACB)
- Tính góc MCN (Tia CN là tia phân giác góc ACM)
- Chỉ ra 2 góc đồng vị bằng nhau.
b)
- Chỉ ra 2 góc so le trong bằng nhau.
Lời giải chi tiết
a)
Ta có: \(\widehat {ACM} + \widehat {ACB} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ACM} + {40^0} = {180^0}\\ \Rightarrow \widehat {ACM} = {180^0} - {40^0}\\ \Rightarrow \widehat {ACM} = {140^0}\end{array}\)
Vì CN là tia phân giác của góc ACM nên
\(\widehat {ACN} = \widehat {NCM} = \dfrac{{\widehat {ACM}}}{2} = \dfrac{{{{140}^0}}}{2} = {70^0}\)
\( \Rightarrow \widehat {ABC} = \widehat {MCN} (= {70^0})\)
Mà 2 góc này ở vị trí đồng vị nên \(CN// AB\).
b)
Theo câu a) \(CN//AB\) nên \(\widehat A = \widehat {ACN}\) (2 góc so le trong). Mà \( \widehat {ACN}= {70^0}\) nên \(\widehat A =70^0\)
Bài 3.35 trang 49 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về:
Dưới đây là đề bài chi tiết:
(Đề bài sẽ được chèn vào đây - ví dụ: Cho hình vẽ, biết góc AOB = 40 độ. Tính số đo các góc còn lại.)
Để giải bài 3.35 trang 49, chúng ta sẽ tiến hành theo các bước sau:
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, các phép tính và giải thích rõ ràng.)
Giả sử đề bài yêu cầu tính góc COD, biết góc AOB = 40 độ và góc AOD = 140 độ. Ta có:
Góc COD = Góc AOD - Góc AOC
Mà góc AOC = Góc AOB + Góc BOC (vì góc BOC là góc kề bù với góc AOB)
Do đó, góc COD = Góc AOD - (Góc AOB + Góc BOC)
(Tiếp tục giải thích và tính toán để tìm ra giá trị của góc COD.)
Khi giải bài tập về các góc tạo bởi đường thẳng cắt đường thẳng, cần chú ý:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Bài 3.35 trang 49 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!