Bài 3.2 trang 37 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.2 trang 37 sách bài tập Toán 7 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình 3.5 a) Gọi tên các cặp góc đối đỉnh.
Đề bài
Cho hình 3.5
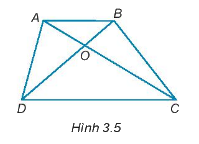
a) Gọi tên các cặp góc đối đỉnh.
b) Gọi tên góc kề bù với \(\widehat {AOD}\)
Phương pháp giải - Xem chi tiết
- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối một cạnh của góc kia.
Lời giải chi tiết
a) Các cặp góc đối đỉnh là \(\widehat {AOB}\) và \(\widehat {DOC}\), \(\widehat {AOD}\) và \(\widehat {BOC}\).
b) Góc kề bù với \(\widehat {AOD}\) là \(\widehat {AOB}\) và \(\widehat {DOC}\).
Bài 3.2 trang 37 sách bài tập Toán 7 Kết nối tri thức yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, bao gồm cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về phép toán với số hữu tỉ, đặc biệt là quy tắc dấu.
Phần a của bài 3.2 thường yêu cầu học sinh tính giá trị của các biểu thức chứa số hữu tỉ. Để giải phần này, học sinh cần thực hiện các phép tính theo đúng thứ tự ưu tiên: trong ngoặc trước, nhân chia trước, cộng trừ sau.
Ví dụ:
Phần b của bài 3.2 thường yêu cầu học sinh tìm giá trị của x trong một phương trình chứa số hữu tỉ. Để giải phần này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng x = một số hữu tỉ.
Ví dụ:
Giả sử bài 3.2 trang 37 có nội dung sau:
a) Tính: (3/4) + (1/8) - (1/2)
b) Tìm x: x * (2/5) = (3/10)
Giải:
a) (3/4) + (1/8) - (1/2) = (6/8) + (1/8) - (4/8) = (6+1-4)/8 = 3/8
b) x * (2/5) = (3/10) => x = (3/10) : (2/5) = (3/10) * (5/2) = (3*5)/(10*2) = 15/20 = 3/4
Để củng cố kiến thức về số hữu tỉ, học sinh có thể tự giải các bài tập tương tự sau:
Bài 3.2 trang 37 sách bài tập Toán 7 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và thực hành thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự.
| Phép toán | Quy tắc |
|---|---|
| Cộng, trừ phân số | Quy đồng mẫu số, cộng/trừ tử số |
| Nhân phân số | Nhân tử số với tử số, mẫu số với mẫu số |
| Chia phân số | Nhân phân số thứ nhất với nghịch đảo của phân số thứ hai |