Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các câu hỏi trắc nghiệm trang 59 sách bài tập Toán 7 Kết nối tri thức với cuộc sống. Chúng tôi giúp bạn hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải quyết vấn đề.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những bài giải dễ hiểu, logic và đầy đủ.
1. Tìm phương án Sai trong câu sau: Trong tam giác
Tìm phương án Sai trong câu sau: Trong tam giác
A.đối diện với góc lớn nhất là cạnh lớn nhất
B.đối diện với cạnh bé nhất là góc nhọn
C.đối diện với cạnh lớn nhất là góc tù
D.đối diện với góc tù (nếu có) là cạnh lớn nhất.
Phương pháp giải:
Quan hệ giữa góc và cạnh đối diện trong một tam giác
Lời giải chi tiết:
Chọn C
Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?
A.7, 5, 7 | B.7, 7, 7 | C.3, 5, 4 | D.4, 7, 3 |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Nếu cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lại thì bộ ba số có là độ dài ba cạnh của một tam giác.
Lời giải chi tiết:
4 + 3 = 7 => Bộ ba số 4,7,3 không là độ dài ba cạnh của một tam giác.
Chọn D
Với mọi tam giác ta đều có:
A.mỗi cạnh lớn hơn nửa chu vi
B.mỗi cạnh lớn hơn hoặc bằng nửa chu vi
C.mỗi cạnh nhỏ hơn nửa chu vi
D.cả ba trường hợp trên đều có thể xảy ra.
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Lời giải chi tiết:
Ba cạnh bất kì trong tam giác:a, b, c
Theo bất đẳng thức tam giác: a < b + c =>a + a < a + b + c
Vậy mỗi cạnh nhỏ hơn nửa chu vi.
Tam giác cân có độ dài cạnh bên b, độ dài cạnh đáy d thì ta phải có:
A.d > b | B.d = 2b | C.d < b/2 | D. d < 2b |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Trong tam giác cân, 2 cạnh bên bằng nhau
Lời giải chi tiết:
Tam giác có 2 cạnh bên là b, áp dụng bất đẳng thức trong tam giác:
b + b > d => 2b > d.
Chọn D
Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?
A.5 cm | B.5,5 cm | C.6 cm | D.6,5 cm |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Tính chất trọng tâm tam giác
Lời giải chi tiết:
G là trọng tâm tam giác ABC
Xét tam giác GBC có GB + GC > BC ( Bất đẳng thức tam giác)
\(\begin{array}{l} \Rightarrow \dfrac{2}{3}\left( {BM + CN} \right) > BC\\ \Rightarrow BM + CN > \dfrac{3}{2}BC = 6\end{array}\)
Chọn D.
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
A.\({120^0}\) | B. \({125^0}\) | C. \({130^0}\) | D. \({135^0}\) |
Phương pháp giải:
Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.
Lời giải chi tiết:
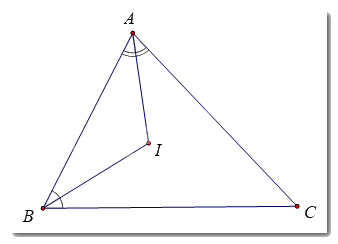
Ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)(Tổng ba góc trong tam giác)
Mà \(\widehat A = \widehat B + \widehat C\)
\(\begin{array}{l} \Rightarrow \left( {\widehat B + \widehat C} \right) + \widehat B + \widehat C = {180^0}\\ \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^0}\\ \Rightarrow \widehat B + \widehat C = {180^0}:2 = {90^0}\\ \Rightarrow \widehat A = \widehat B + \widehat C = {90^0}\end{array}\)
Xét tam giác BIC có:
\(\widehat {BIC} = {180^0} - \left( {\widehat {\dfrac{B}{2}} + \dfrac{{\widehat C}}{2}} \right) = {180^0} - \dfrac{{{{90}^0}}}{2} = {180^0} - {45^0} = {135^0}\).
Chọn D.
Tìm phương án Sai trong câu sau: Trong tam giác
A.đối diện với góc lớn nhất là cạnh lớn nhất
B.đối diện với cạnh bé nhất là góc nhọn
C.đối diện với cạnh lớn nhất là góc tù
D.đối diện với góc tù (nếu có) là cạnh lớn nhất.
Phương pháp giải:
Quan hệ giữa góc và cạnh đối diện trong một tam giác
Lời giải chi tiết:
Chọn C
Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?
A.7, 5, 7 | B.7, 7, 7 | C.3, 5, 4 | D.4, 7, 3 |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Nếu cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lại thì bộ ba số có là độ dài ba cạnh của một tam giác.
Lời giải chi tiết:
4 + 3 = 7 => Bộ ba số 4,7,3 không là độ dài ba cạnh của một tam giác.
Chọn D
Tam giác cân có độ dài cạnh bên b, độ dài cạnh đáy d thì ta phải có:
A.d > b | B.d = 2b | C.d < b/2 | D. d < 2b |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Trong tam giác cân, 2 cạnh bên bằng nhau
Lời giải chi tiết:
Tam giác có 2 cạnh bên là b, áp dụng bất đẳng thức trong tam giác:
b + b > d => 2b > d.
Chọn D
Với mọi tam giác ta đều có:
A.mỗi cạnh lớn hơn nửa chu vi
B.mỗi cạnh lớn hơn hoặc bằng nửa chu vi
C.mỗi cạnh nhỏ hơn nửa chu vi
D.cả ba trường hợp trên đều có thể xảy ra.
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Lời giải chi tiết:
Ba cạnh bất kì trong tam giác:a, b, c
Theo bất đẳng thức tam giác: a < b + c =>a + a < a + b + c
Vậy mỗi cạnh nhỏ hơn nửa chu vi.
Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?
A.5 cm | B.5,5 cm | C.6 cm | D.6,5 cm |
Phương pháp giải:
Áp dụng bất đẳng thức tam giác
Tính chất trọng tâm tam giác
Lời giải chi tiết:
G là trọng tâm tam giác ABC
Xét tam giác GBC có GB + GC > BC ( Bất đẳng thức tam giác)
\(\begin{array}{l} \Rightarrow \dfrac{2}{3}\left( {BM + CN} \right) > BC\\ \Rightarrow BM + CN > \dfrac{3}{2}BC = 6\end{array}\)
Chọn D.
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
A.\({120^0}\) | B. \({125^0}\) | C. \({130^0}\) | D. \({135^0}\) |
Phương pháp giải:
Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.
Lời giải chi tiết:
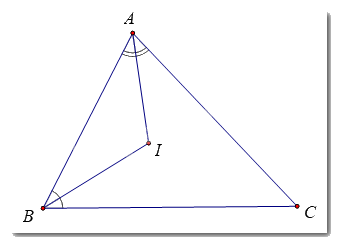
Ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)(Tổng ba góc trong tam giác)
Mà \(\widehat A = \widehat B + \widehat C\)
\(\begin{array}{l} \Rightarrow \left( {\widehat B + \widehat C} \right) + \widehat B + \widehat C = {180^0}\\ \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^0}\\ \Rightarrow \widehat B + \widehat C = {180^0}:2 = {90^0}\\ \Rightarrow \widehat A = \widehat B + \widehat C = {90^0}\end{array}\)
Xét tam giác BIC có:
\(\widehat {BIC} = {180^0} - \left( {\widehat {\dfrac{B}{2}} + \dfrac{{\widehat C}}{2}} \right) = {180^0} - \dfrac{{{{90}^0}}}{2} = {180^0} - {45^0} = {135^0}\).
Chọn D.
Trang 59 sách bài tập Toán 7 Kết nối tri thức với cuộc sống chứa đựng những bài tập trắc nghiệm quan trọng, giúp học sinh củng cố kiến thức về các khái niệm đã học trong chương. Việc giải đúng các câu hỏi này không chỉ giúp học sinh đạt điểm cao trong các bài kiểm tra mà còn tạo nền tảng vững chắc cho việc học tập các kiến thức toán học nâng cao hơn.
Trang 59 tập trung vào việc ôn tập và củng cố các kiến thức về:
Dưới đây là hướng dẫn giải chi tiết từng câu hỏi trắc nghiệm trang 59 sách bài tập Toán 7 Kết nối tri thức với cuộc sống:
Đáp án: ...
Giải thích: ...
Đáp án: ...
Giải thích: ...
Đáp án: ...
Giải thích: ...
Để giải nhanh và chính xác các bài tập trắc nghiệm, bạn có thể áp dụng một số mẹo sau:
Ví dụ: Cho hai số hữu tỉ a = -2/3 và b = 1/2. Tính a + b.
Giải: a + b = -2/3 + 1/2 = -4/6 + 3/6 = -1/6
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Việc giải bài tập trắc nghiệm không chỉ giúp bạn làm quen với cấu trúc đề thi mà còn giúp bạn rèn luyện khả năng tư duy logic, phân tích và đánh giá thông tin. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong nhiều lĩnh vực khác của cuộc sống.
Hy vọng với hướng dẫn chi tiết và dễ hiểu này, bạn sẽ tự tin giải quyết các câu hỏi trắc nghiệm trang 59 sách bài tập Toán 7 Kết nối tri thức với cuộc sống. Chúc bạn học tập tốt và đạt kết quả cao!
| Câu hỏi | Đáp án | Giải thích |
|---|---|---|
| Câu 1 | ... | ... |
| Câu 2 | ... | ... |