Bài 5.13 trang 82 sách bài tập Toán 7 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tam giác cân vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.13 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Kết quả của một khảo sát về mục đích vào mạng Internet của học sinh cấp THCS được cho trong hình 5.5 a) Lập bảng thống kê biểu diễn tỉ lệ học sinh cấp THCS theo mục đích vào mạng Internet. b) Trong số 500 học sinh trường A vào mạng Internet có khoảng bao nhiêu em vào với mục đích phục vụ học tập?
Đề bài
Kết quả của một khảo sát về mục đích vào mạng Internet của học sinh cấp THCS được cho trong hình 5.5
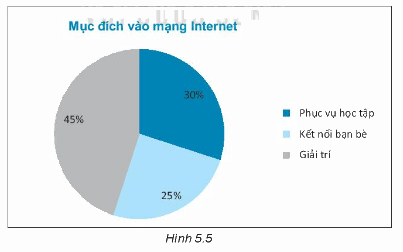
a) Lập bảng thống kê biểu diễn tỉ lệ học sinh cấp THCS theo mục đích vào mạng Internet.
b) Trong số 500 học sinh trường A vào mạng Internet có khoảng bao nhiêu em vào với mục đích phục vụ học tập?
Lời giải chi tiết
a)
Bảng thống kê
Mục đích | Phục vụ học tập | Kết nối bạn bè | Giải trí |
Tỉ lệ | 30% | 25% | 45% |
b)
Số học sinh vào mạng Internet với mục đích phục vụ học tập là:
\(500.30\%=150\) (học sinh)
Vậy có khoảng 150 học sinh vào Internet vào mục đích phục vụ học tập.
Bài 5.13 trang 82 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về tam giác cân, tính chất đường trung tuyến, đường cao, đường phân giác để giải quyết các bài toán liên quan đến hình học.
Cho tam giác ABC cân tại A. Gọi D là trung điểm của BC.
a) Chứng minh AD là đường trung tuyến của tam giác ABC:
Vì D là trung điểm của BC (theo giả thiết) nên BD = DC. Đường thẳng AD nối đỉnh A với trung điểm D của cạnh BC, do đó AD là đường trung tuyến của tam giác ABC.
b) Chứng minh AD là đường cao của tam giác ABC:
Vì tam giác ABC cân tại A (theo giả thiết) nên AB = AC. Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c-g-c). Suy ra ∠ADB = ∠ADC. Mà ∠ADB + ∠ADC = 180° (kề bù) nên ∠ADB = ∠ADC = 90°. Vậy AD vuông góc với BC tại D, do đó AD là đường cao của tam giác ABC.
c) Chứng minh AD là đường phân giác của tam giác ABC:
Vì tam giác ABC cân tại A (theo giả thiết) nên ∠B = ∠C. Xét tam giác ABD và tam giác ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c-g-c). Suy ra ∠BAD = ∠CAD. Vậy AD là đường phân giác của tam giác ABC.
Qua bài giải trên, ta đã chứng minh được rằng trong một tam giác cân, đường trung tuyến, đường cao, đường phân giác kẻ từ đỉnh góc cân đều là một. Đây là một tính chất quan trọng cần ghi nhớ khi học về tam giác cân.
Để hiểu rõ hơn về tam giác cân, các em có thể tìm hiểu thêm về các tính chất sau:
Việc nắm vững các kiến thức này sẽ giúp các em giải quyết các bài toán liên quan đến tam giác cân một cách dễ dàng và hiệu quả hơn.
Các em có thể luyện tập thêm với các bài tập tương tự trong sách bài tập Toán 7 - Kết nối tri thức để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 5.13 trang 82 sách bài tập Toán 7 - Kết nối tri thức với cuộc sống và đạt kết quả tốt trong học tập.