Bài 10 trang 163 Tài liệu dạy – học toán 6 tập 1

Bài 10 trang 163 Tài liệu dạy – học toán 6 tập 1: Giải chi tiết

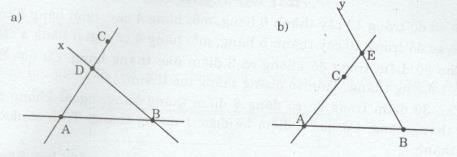
Bài 10 trang 163 Tài liệu dạy – học toán 6 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép tính với số nguyên, đặc biệt là phép cộng, trừ, nhân, chia số nguyên. Bài tập này thường yêu cầu học sinh vận dụng các quy tắc về dấu của số nguyên để thực hiện các phép tính một cách chính xác.

Nội dung bài tập

Bài 10 thường bao gồm các dạng bài tập sau:

• Tính giá trị của biểu thức: Học sinh cần thực hiện các phép tính theo đúng thứ tự ưu tiên (ngoặc, nhân chia trước, cộng trừ sau) và chú ý đến quy tắc dấu.
• Tìm x: Học sinh cần giải phương trình đơn giản để tìm giá trị của ẩn x.
• Bài toán thực tế: Bài tập có thể được đặt trong một ngữ cảnh thực tế để học sinh áp dụng kiến thức vào giải quyết vấn đề.

Hướng dẫn giải chi tiết

Để giải bài 10 trang 163 một cách hiệu quả, học sinh cần:

1. Nắm vững các quy tắc về dấu của số nguyên: (+)+(+) = +, (+)+(-) = ?, (-)+(-) = -, (+)-(-) = +, (-)-(-) = ?, (+).(+) = +, (+).(-) = -, (-).(-) = +.
2. Thực hiện các phép tính theo đúng thứ tự ưu tiên: Sử dụng dấu ngoặc để nhóm các phép tính cần thực hiện trước.
3. Kiểm tra lại kết quả: Đảm bảo rằng kết quả tính toán là chính xác.

Ví dụ minh họa

Ví dụ 1: Tính giá trị của biểu thức: 12 + (-5) - 8

Giải:

12 + (-5) - 8 = 7 - 8 = -1

Ví dụ 2: Tìm x biết: x + 3 = 7

Giải:

x = 7 - 3 = 4

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về số nguyên, học sinh có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi làm bài kiểm tra.

Mở rộng kiến thức

Ngoài các quy tắc cơ bản về dấu của số nguyên, học sinh cũng nên tìm hiểu thêm về các khái niệm liên quan như giá trị tuyệt đối của một số nguyên, số đối của một số nguyên. Việc nắm vững các khái niệm này sẽ giúp học sinh hiểu sâu hơn về số nguyên và ứng dụng chúng vào giải quyết các bài toán phức tạp hơn.

Ứng dụng thực tế

Kiến thức về số nguyên được ứng dụng rộng rãi trong đời sống hàng ngày, ví dụ như:

• Nhiệt độ: Nhiệt độ dưới 0 độ C được biểu diễn bằng số âm.
• Độ cao: Độ cao so với mực nước biển được biểu diễn bằng số dương, còn độ sâu dưới mực nước biển được biểu diễn bằng số âm.
• Tài chính: Khoản nợ được biểu diễn bằng số âm, còn khoản tiền lãi được biểu diễn bằng số dương.

Tổng kết

Bài 10 trang 163 Tài liệu dạy – học toán 6 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số nguyên. Bằng cách nắm vững các quy tắc cơ bản, thực hiện các phép tính theo đúng thứ tự ưu tiên và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập về số nguyên một cách hiệu quả.