Chào mừng các em học sinh lớp 6 đến với lời giải chi tiết Bài 6 trang 145 trong Tài liệu dạy – học toán 6 tập 1. Bài học này tập trung vào việc rèn luyện kỹ năng thực hành các phép tính với số nguyên, đặc biệt là các bài toán liên quan đến việc cộng, trừ, nhân, chia số nguyên.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Trên trục số cho ba điểm x, y, z. Hãy vẽ trên trục số đó các điểm :
Đề bài
Trên trục số cho ba điểm x, y, z. Hãy vẽ trên trục số đó các điểm :

\(\eqalign{ & a) \;- x, - y, - z \cr & b)\;\left| x \right|,\left| y \right|,\left| z \right| \cr & c)\;x + y,x - z,x.y. \cr} \)
Lời giải chi tiết
\(x = 2; y = -3; z = 5.\)
Do đó
\(\eqalign{ & - x = - 2; - y = 3; - z = - 5;\cr&\left| x \right| = 2;\left| y \right| = 3;\left| z \right| = 5;\cr&x - z = 2 - 5 = - 3 \cr & x + y = 2 + ( - 3) = - 1 \cr & x.y = 2.( - 3) = - 6 \cr} \)
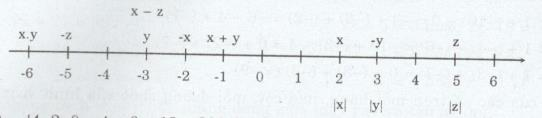
Bài 6 trang 145 Tài liệu dạy – học toán 6 tập 1 là một bài tập thực hành quan trọng giúp học sinh củng cố kiến thức về số nguyên và các phép toán cơ bản. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Để tính biểu thức này, ta áp dụng quy tắc cộng hai số nguyên khác dấu: Cộng hai số nguyên khác dấu, ta lấy số lớn trừ đi số nhỏ và giữ dấu của số lớn. Trong trường hợp này, 12 > 8, nên ta có:
12 + (-8) = 12 - 8 = 4
Tương tự như trên, ta có:
(-5) + 7 = 7 - 5 = 2
Áp dụng quy tắc cộng hai số nguyên cùng dấu: Cộng hai số nguyên cùng dấu, ta cộng các giá trị tuyệt đối của chúng và giữ dấu của hai số đó. Trong trường hợp này, ta có:
(-15) + (-6) = - (15 + 6) = -21
20 + (-10) = 20 - 10 = 10
Đây là phép trừ hai số nguyên. Ta có:
5 - 3 = 2
Để trừ hai số nguyên, ta có thể cộng số trừ với số đối của số bị trừ. Trong trường hợp này, ta có:
(-7) - 2 = (-7) + (-2) = -9
Tương tự, ta có:
10 - (-4) = 10 + 4 = 14
(-12) - (-5) = (-12) + 5 = -7
Quy tắc nhân hai số nguyên: Nhân hai số nguyên cùng dấu, ta nhân các giá trị tuyệt đối của chúng và giữ dấu dương. Nhân hai số nguyên khác dấu, ta nhân các giá trị tuyệt đối của chúng và giữ dấu âm.
2 * (-3) = -6
(-4) * 5 = -20
(-1) * (-7) = 7
0 * (-8) = 0
18 : 3 = 6
(-24) : 4 = -6
(-36) : (-6) = 6
0 : (-5) = 0
Lưu ý: Khi thực hiện các phép toán với số nguyên, cần nắm vững các quy tắc về dấu để đảm bảo tính chính xác của kết quả.
Bài 6 trang 145 Tài liệu dạy – học toán 6 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính toán với số nguyên. Việc nắm vững các quy tắc và thực hành thường xuyên sẽ giúp các em tự tin hơn trong việc giải các bài tập toán học.
Hy vọng với lời giải chi tiết này, các em học sinh lớp 6 sẽ hiểu rõ hơn về bài học và đạt kết quả tốt trong môn Toán.