Bài tập Hoạt động 1 trang 106 trong Tài liệu dạy – học toán 6 tập 2 là một phần quan trọng trong chương trình học. giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi không chỉ cung cấp đáp án mà còn phân tích cách giải, giúp học sinh hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Giải bài tập Hãy đo các góc
Đề bài
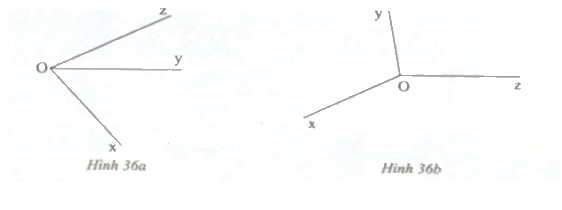
Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong hai hình sau rồi so sánh \(\widehat {xOy} + \widehat {yOz}\) với \(\widehat {xOz}\).
Lời giải chi tiết
Hình 36a) \(\widehat {xOy} = {25^0};\widehat {yOz} = {50^0};\widehat {xOz} = {75^0}.\)
Ta có: \(\widehat {xOy} + \widehat {yOz} = {25^0} + {50^0} = {75^0} \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}({75^0}).\)
Hình 36b) \(\widehat {xOy} = {110^0};\widehat {yOz} = {100^0};\widehat {xOz} = {150^0}.\)
Ta có: \(\widehat {xOy} + \widehat {yOz} = {110^0} + {100^0} = {210^0} \Rightarrow \widehat {xOy} + \widehat {yOz} > \widehat {xOz}\) (vì \({210^0} > {150^0}).\)
Hoạt động 1 trang 106 trong Tài liệu dạy – học Toán 6 tập 2 thường tập trung vào việc củng cố kiến thức về các phép tính với số tự nhiên, các khái niệm về bội và ước, hoặc các bài toán liên quan đến hình học cơ bản. Mục tiêu chính của hoạt động này là giúp học sinh vận dụng kiến thức đã học vào giải quyết các tình huống thực tế, phát triển tư duy logic và kỹ năng giải quyết vấn đề.
Tùy thuộc vào từng chương cụ thể, Hoạt động 1 trang 106 có thể bao gồm các dạng bài tập sau:
Để giải quyết các bài tập trong Hoạt động 1 trang 106 một cách hiệu quả, học sinh cần:
Bài tập: Tính giá trị của biểu thức: 12 + 5 x 3 - 8 : 2
Lời giải:
Khi giải các bài tập trong Hoạt động 1 trang 106, học sinh cần lưu ý:
Ngoài Tài liệu dạy – học Toán 6 tập 2, học sinh có thể tham khảo thêm các tài nguyên sau để hỗ trợ học tập:
Hoạt động 1 trang 106 Toán 6 Tập 2 là một cơ hội tốt để học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp, và thực hành thường xuyên, học sinh có thể tự tin giải quyết các bài tập và đạt kết quả tốt trong môn Toán.