Chào mừng các em học sinh đến với bài học về Lý thuyết Điểm và đường thẳng trong chương trình Toán 6 KNTT. Bài học này sẽ giúp các em hiểu rõ các khái niệm cơ bản về điểm, đường thẳng, mối quan hệ giữa chúng và ứng dụng trong thực tế cuộc sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng được thiết kế trực quan, dễ hiểu, cùng với các bài tập đa dạng để các em có thể luyện tập và củng cố kiến thức.
Lý thuyết Điểm và đường thẳng Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
1.Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
*Điểm
Dấu chấm nhỏ là hình ảnh của điểm
Quy ước: Khi nói 2 điểm mà không nói gì thêm, ta hiểu đó là 2 điểm phân biệt
*Đường thẳng
Đường thẳng không bị giới hạn về 2 phía
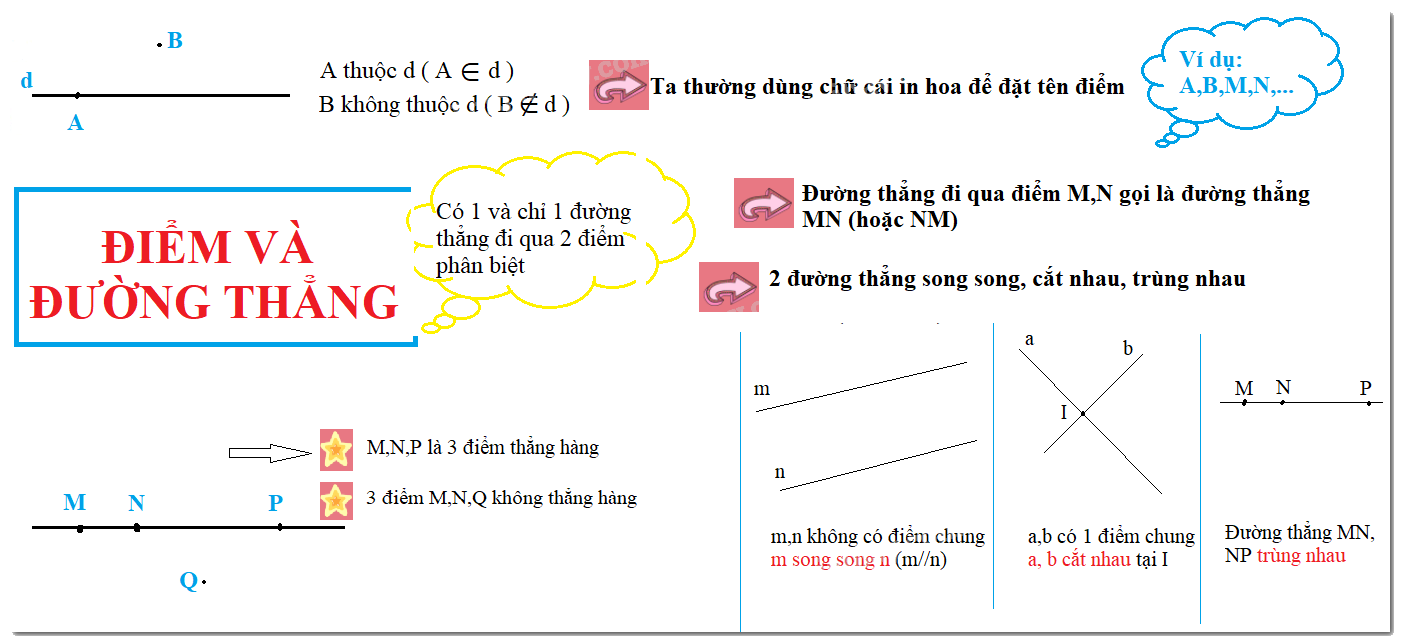
*Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
Ta thường dùng chữ cái in hoa để đặt tên điểm và chữ cái thường để đặt tên đường thẳng, chẳng hạn điểm M,N,P,Q,...; đường thẳng a,b,d,...
Điểm A thuộc đường thẳng d, kí hiệu \(A \in d\)
Điểm B không đường thẳng d, kí hiệu là \(B \notin d\)
Nếu \(A \in d\), ta còn nói: Điểm A nằm trên đường thẳng d, hay đường thẳng d đi qua điểm A
Chú ý: Có vô số điểm thuộc đường thẳng
*Đường thẳng đi qua 2 điểm
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm A và B
Đường thẳng đi qua 2 điểm A, B được gọi đường thẳng AB hay đường thẳng BA
2. Ba điểm thẳng hàng
• Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.
• Ba điểm phân biệt D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.
Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
3. Hai đường thẳng song song, cắt nhau, trùng nhau
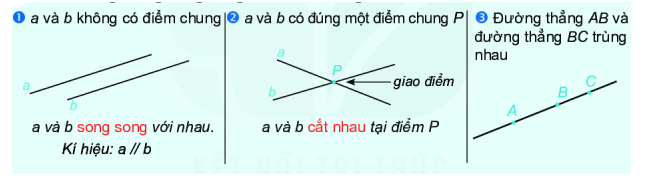
Trong chương trình Toán 6 KNTT, kiến thức về điểm và đường thẳng là nền tảng quan trọng để xây dựng các khái niệm hình học phức tạp hơn. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, kết hợp với các ví dụ minh họa và ứng dụng thực tế để giúp học sinh hiểu sâu sắc hơn.
Điểm là một khái niệm cơ bản trong hình học, được hiểu là vị trí xác định. Chúng ta không thể mô tả chính xác kích thước của điểm, mà chỉ có thể xác định vị trí của nó. Trong thực tế, chúng ta thường biểu diễn điểm bằng một chấm nhỏ trên giấy hoặc màn hình.
Đường thẳng là một đường không có giới hạn, kéo dài vô tận theo hai hướng. Một đường thẳng được xác định bởi hai điểm phân biệt. Chúng ta thường biểu diễn đường thẳng bằng một mũi tên hai chiều.
Có ba trường hợp xảy ra khi xét mối quan hệ giữa một điểm và một đường thẳng:
Ngoài khái niệm cơ bản, chúng ta còn gặp một số khái niệm liên quan đến đường thẳng:
Lý thuyết về điểm và đường thẳng không chỉ quan trọng trong toán học mà còn có nhiều ứng dụng trong cuộc sống hàng ngày:
Để củng cố kiến thức về lý thuyết điểm và đường thẳng, chúng ta hãy cùng giải một số bài tập sau:
Lý thuyết về điểm và đường thẳng là một phần quan trọng của chương trình Toán 6 KNTT. Việc nắm vững kiến thức này sẽ giúp học sinh có một nền tảng vững chắc để học các khái niệm hình học phức tạp hơn. Hy vọng rằng bài viết này đã cung cấp cho các em một cái nhìn toàn diện và dễ hiểu về lý thuyết này.
| Khái niệm | Mô tả |
|---|---|
| Điểm | Vị trí xác định |
| Đường thẳng | Đường không có giới hạn |
| Đoạn thẳng | Phần của đường thẳng giới hạn bởi hai điểm |
| Tia | Phần của đường thẳng có một điểm đầu |